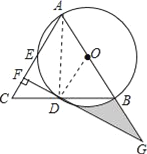
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

参考答案:
【答案】(1)见解析(2)2![]() ﹣
﹣![]() π.
π.
【解析】(1)连接AD、OD,由AB为直径可得出点D为BC的中点,由此得出OD为△BAC的中位线,再根据中位线的性质即可得出OD⊥DF,从而证出DF是⊙O的切线;
(2)CF=1,DF=![]() ,通过解直角三角形得出CD=2、∠C=60°,从而得出△ABC为等边三角形,再利用分割图形求面积法即可得出阴影部分的面积.
,通过解直角三角形得出CD=2、∠C=60°,从而得出△ABC为等边三角形,再利用分割图形求面积法即可得出阴影部分的面积.
(1)证明:连接AD、OD,如图所示.
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AC=AB,
∴点D为线段BC的中点.
∵点O为AB的中点,
∴OD为△BAC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线.
(2)解:在Rt△CFD中,CF=1,DF=![]() ,
,
∴tan∠C=![]() =
=![]() ,CD=2,
,CD=2,
∴∠C=60°,
∵AC=AB,
∴△ABC为等边三角形,
∴AB=4.
∵OD∥AC,
∴∠DOG=∠BAC=60°,
∴DG=ODtan∠DOG=2![]() ,
,
∴S阴影=S△ODG﹣S扇形OBD=![]() DGOD﹣
DGOD﹣![]() πOB2=2
πOB2=2![]() ﹣
﹣![]() π.
π.
“点睛”本题考查了等腰三角形的性质、切线的判定、扇形面积的计算以及三角形面积的计算,解题的关键是:(1)证出OD⊥DF;(2)利用分割图形求面积求出阴影部分的面积.本题属于中档题,难度不大,解决该题型题目时,利用分割图形求面积法是解题的难点,在日常练习中应加强训练.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下说法错误的是( )
A.两直线平行,内错角相等B.两直线平行,同旁内角相等
C.同位角相等,两直线平行D.对顶角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x﹣y=7,xy=2,则x2+y2的值为( )
A.53
B.45
C.47
D.51 -
科目: 来源: 题型:
查看答案和解析>>【题目】某种原子质量为0.00001992g,用科学记数法表示为______g.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费y元.
(1)分别求出0≤x≤200和x>200时,y与x的函数表达式;
(2)小明家5月份交纳电费117元,小明家这个月用电多少度? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售A,B两种商品,已知销售一件A种商品可获利润10元,销售一件B种商品可获利润15元.
(1)该商店销售A,B两种商品共100件,获利润1350元,则A,B两种商品各销售多少件?
(2)根据市场需求,该商店准备购进A,B两种商品共200件,其中B种商品的件数不多于A种商品件数的3倍.为了获得最大利润,应购进A,B两种商品各多少件?可获得最大利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC垂足为点D,AD是BC边上的中线,BE⊥AC,垂足为点E.则以下4个结论:①AB=AC;②∠EBC=
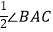 ;③AE=CE;④∠EBC=
;③AE=CE;④∠EBC= 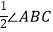 中正确的有( )
中正确的有( )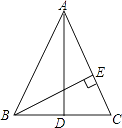
A.①②
B.②③
C.①②③
D.①②③④
相关试题

