【题目】如图,线段MN是周长为36cm的圆的直径(圆心为O),动点A从点M出发,以![]() 的速度沿顺时针方向在圆周上运动,经过点N时,其速度变为
的速度沿顺时针方向在圆周上运动,经过点N时,其速度变为![]() ,并以这个速度继续沿顺时针方向运动之点M后停止。在动点A运动的同时,动点B从点N出发,以
,并以这个速度继续沿顺时针方向运动之点M后停止。在动点A运动的同时,动点B从点N出发,以![]() 的速度沿逆时针方向在圆周上运动,绕一周后停止运动。设点A、点B运动时间为
的速度沿逆时针方向在圆周上运动,绕一周后停止运动。设点A、点B运动时间为![]() .
.
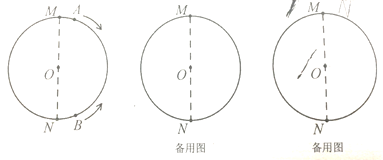
(1)连接OA、OB,当t=4时,![]() = °,在整个运动过程中,当
= °,在整个运动过程中,当![]() 时,点A运动的路程为 cm(第2空结果用含t的式子表示);
时,点A运动的路程为 cm(第2空结果用含t的式子表示);
(2)当A、B两点相遇时,求运动时间t;
(3)连接OA、OB,当![]() 时,请直接写出所有符合条件的运动时间t.
时,请直接写出所有符合条件的运动时间t.
参考答案:
【答案】(1)20;![]() ;(2)当A、B两点相遇时,t=
;(2)当A、B两点相遇时,t=![]() 或
或![]() ;(3)当
;(3)当![]() 时,t=3或
时,t=3或![]() 或12或
或12或![]()
【解析】
(1)根据圆O的周长,即可求出半圆![]() 的长,然后求出当t=4时,点A的运动路程
的长,然后求出当t=4时,点A的运动路程![]() 和点B的运动路程
和点B的运动路程![]() ,即可求出
,即可求出![]() ,然后求出
,然后求出![]() 占圆周长的分率乘360°即可求出
占圆周长的分率乘360°即可求出![]() ,画出
,画出![]() ,根据点A行驶的路程
,根据点A行驶的路程![]() =半圆
=半圆![]() +
+![]() 和速度即可求出结论;
和速度即可求出结论;
(2)根据第一次相遇和第二次相遇分类讨论,分别画出对应的图形,然后根据图形找出等量关系即可求出t的值;
(3)根据第一次相遇前![]() 、第一次相遇后
、第一次相遇后![]() 、第二次相遇前
、第二次相遇前![]() 、第二次相遇后
、第二次相遇后![]() ,分类讨论分别画出对应的图形,然后根据图形找出等量关系即可求出t的值.
,分类讨论分别画出对应的图形,然后根据图形找出等量关系即可求出t的值.
解:(1)∵圆O的周长为36cm
∴半圆![]() 的长为36÷2=18cm
的长为36÷2=18cm
当t=4时,根据题意可得![]() =3×4=12cm,
=3×4=12cm,![]() =2×4=8cm,如下图所示
=2×4=8cm,如下图所示

∴![]() =
=![]() +
+![]() -半圆
-半圆![]() =2cm
=2cm
∴∠AOB=![]()
点A到点N所需时间为18÷3=6s
当![]() 时,如下图所示
时,如下图所示

点A行驶的路程![]() =半圆
=半圆![]() +
+![]() =18+
=18+![]() =
=![]()
故答案为:20;![]() .
.
(2)当A、B两点第一次相遇时,如下图所示:
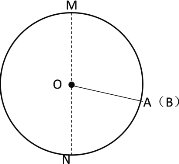
此时![]() +
+![]() =半圆
=半圆![]()
∴3t+2t=18
解得:t=![]() ;
;
当A、B两点第二次相遇时,如下图所示:

此时![]() +
+![]() -半圆
-半圆![]() =圆O的周长
=圆O的周长
即![]() +2t-18=36
+2t-18=36
解得:t=![]()
综上所述:当A、B两点相遇时,t=![]() 或
或![]() ;
;
(3)①当点A、B第一次相遇之前,∠AOB=30°时,如下图所示

此时![]() +
+![]() +
+![]() =半圆
=半圆![]()
即3t+![]() +2t=18
+2t=18
解得:t=3;
②当点A、B第一次相遇之后,∠AOB=30°时,如下图所示

此时![]() -
-![]() +
+![]() =半圆
=半圆![]()
即3t-![]() +2t=18
+2t=18
解得:t=![]() ;
;
③当点A、B第二次相遇之前,∠AOB=30°时,如下图所示
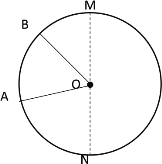
此时![]() +
+![]() -半圆
-半圆![]() +
+![]() =圆O的周长
=圆O的周长
即![]() +2t-18+
+2t-18+![]() =36
=36
解得:t=12;
④当点A、B第二次相遇之后,∠AOB=30°时,如下图所示
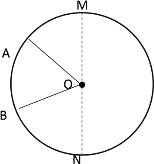
此时![]() +
+![]() -半圆
-半圆![]() -
-![]() =圆O的周长
=圆O的周长
即![]() +2t-18-
+2t-18-![]() =36
=36
解得:t=![]() ;
;
综上所述:当![]() 时,t=3或
时,t=3或![]() 或12或
或12或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
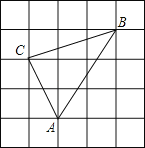
(1)△ABC的周长;
(2)请判断三角形ABC是否是直角三角形,并说明理由;
(3)△ABC的面积;
(4)点C到AB边的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请补充完成以下解答过程,并在括号内填写该步骤的理由.已知:如图,
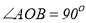 ,
,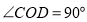 ,OA平分
,OA平分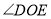 ,若
,若 ,求
,求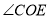 的度数.
的度数.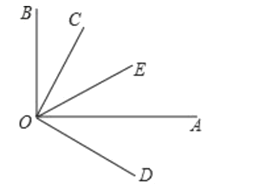
解:因为
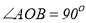 ,
,所以
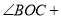 ________
________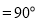 .
.因为_________
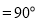 ,
,所以
 .
.所以
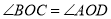 .(__________________)
.(__________________)因为
 ,
,所以
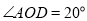 .
.因为OA平分
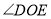 ,
,所以__________
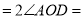 _______°
_______°所以
 _______°.
_______°. -
科目: 来源: 题型:
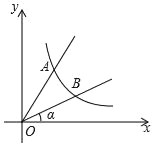
查看答案和解析>>【题目】如图,直线y=2x与反比例函数y=
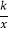 (k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=
(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα= .
.(1)求k的值及点B坐标.
(2)连接AB,求三角形AOB的面积S△AOB.
-
科目: 来源: 题型:
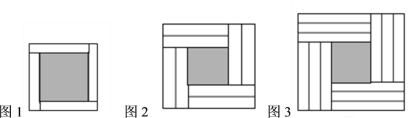
查看答案和解析>>【题目】用若干个形状、大小完全相同的长方形纸片围成正方形,4个长方形纸片围成如图1所示的正方形,其涂色部分的面积是25;8个长方形纸片围成如图2所示的正方形,其涂色部分的面积是16;12个长方形纸片围成如图3所示的正方形,其涂色部分的面积是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“3倍角三角形”例如:一个三角形三个内角的度数分别是
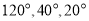 ,这个三角形就是一个“3倍角三角形”.反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
,这个三角形就是一个“3倍角三角形”.反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.(1)如图1,已知
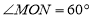 ,在射线
,在射线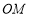 上取一点
上取一点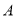 ,过点
,过点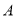 作
作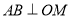 交
交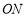 于点
于点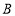 .判断
.判断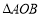 是否是“3倍角三角形”,为什么?
是否是“3倍角三角形”,为什么?(2)在(1)的条件下,以
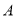 为端点画射线
为端点画射线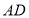 ,交线段
,交线段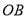 于点
于点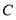 (点
(点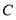 不与点
不与点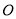 、点
、点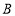 重合).若
重合).若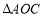 是“3倍角三角形”,求
是“3倍角三角形”,求 的度数.
的度数.(3)如图2,点
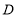 在
在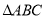 的边上,连接
的边上,连接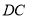 ,作
,作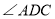 的平分线交
的平分线交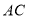 于点
于点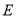 ,在
,在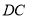 上取一点
上取一点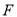 ,使得
,使得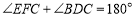 ,
,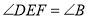 .若
.若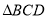 是“3倍角三角形”,求
是“3倍角三角形”,求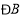 的度数.
的度数.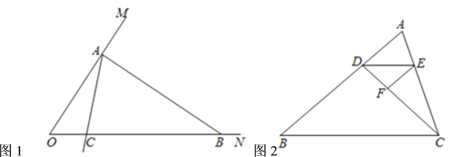
相关试题

