【题目】阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“3倍角三角形”例如:一个三角形三个内角的度数分别是![]() ,这个三角形就是一个“3倍角三角形”.反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
,这个三角形就是一个“3倍角三角形”.反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
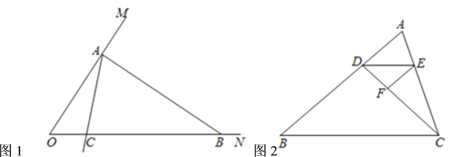
(1)如图1,已知![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .判断
.判断![]() 是否是“3倍角三角形”,为什么?
是否是“3倍角三角形”,为什么?
(2)在(1)的条件下,以![]() 为端点画射线
为端点画射线![]() ,交线段
,交线段![]() 于点
于点![]() (点
(点![]() 不与点
不与点![]() 、点
、点![]() 重合).若
重合).若![]() 是“3倍角三角形”,求
是“3倍角三角形”,求![]() 的度数.
的度数.
(3)如图2,点![]() 在
在![]() 的边上,连接
的边上,连接![]() ,作
,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,![]() .若
.若![]() 是“3倍角三角形”,求
是“3倍角三角形”,求![]() 的度数.
的度数.
参考答案:
【答案】(1)是,理由详见解析;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据“3倍角三角形”的定义进行判断即可得出答案;
(2)根据“3倍角三角形”的定义,分两种情况:当![]() 时, 当
时, 当![]() ,
,![]() 都是“3倍角三角形”,分别进行讨论即可;
都是“3倍角三角形”,分别进行讨论即可;
(3)根据平行线的性质可得出![]() ,然后利用角平分线的定义有
,然后利用角平分线的定义有![]() ,根据等量代换有
,根据等量代换有![]() ,再根据
,再根据![]() 是“3倍角三角形”,则有
是“3倍角三角形”,则有![]() 或
或![]() 两种情况,最后根据三角形内角和求出
两种情况,最后根据三角形内角和求出![]() 的度数即可.
的度数即可.
解:(1)是,
理由:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为“3倍角三角形”.
为“3倍角三角形”.
(2)![]()
![]() 当
当![]() 时,
时,![]() 是“3倍角三角形”,
是“3倍角三角形”,
此时![]()
![]()
当![]() ,
,![]() 是“3倍角三角形”
是“3倍角三角形”
此时![]() ,
,
![]()
![]() ;
;
(3)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() 是“3倍角三角形”,
是“3倍角三角形”,
![]() 或
或![]() ,
,
![]() ,
,
![]() 或
或![]() .
.
-
科目: 来源: 题型:
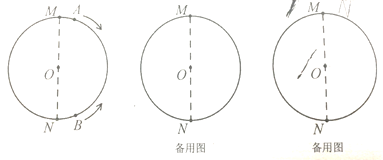
查看答案和解析>>【题目】如图,线段MN是周长为36cm的圆的直径(圆心为O),动点A从点M出发,以
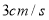 的速度沿顺时针方向在圆周上运动,经过点N时,其速度变为
的速度沿顺时针方向在圆周上运动,经过点N时,其速度变为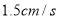 ,并以这个速度继续沿顺时针方向运动之点M后停止。在动点A运动的同时,动点B从点N出发,以
,并以这个速度继续沿顺时针方向运动之点M后停止。在动点A运动的同时,动点B从点N出发,以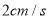 的速度沿逆时针方向在圆周上运动,绕一周后停止运动。设点A、点B运动时间为
的速度沿逆时针方向在圆周上运动,绕一周后停止运动。设点A、点B运动时间为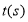 .
.
(1)连接OA、OB,当t=4时,
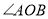 = °,在整个运动过程中,当
= °,在整个运动过程中,当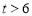 时,点A运动的路程为 cm(第2空结果用含t的式子表示);
时,点A运动的路程为 cm(第2空结果用含t的式子表示);(2)当A、B两点相遇时,求运动时间t;
(3)连接OA、OB,当
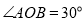 时,请直接写出所有符合条件的运动时间t.
时,请直接写出所有符合条件的运动时间t. -
科目: 来源: 题型:
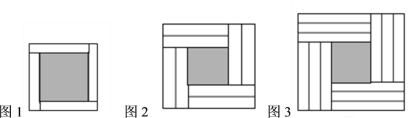
查看答案和解析>>【题目】用若干个形状、大小完全相同的长方形纸片围成正方形,4个长方形纸片围成如图1所示的正方形,其涂色部分的面积是25;8个长方形纸片围成如图2所示的正方形,其涂色部分的面积是16;12个长方形纸片围成如图3所示的正方形,其涂色部分的面积是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①符号相反的数互为相反数;②
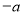 一定是一个负数;③正整数、负整数统称为整数;④一个数的绝对值越大,表示它的点在数轴上离原点越远;⑤当
一定是一个负数;③正整数、负整数统称为整数;④一个数的绝对值越大,表示它的点在数轴上离原点越远;⑤当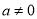 时,
时,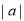 总是大于0,正确的有( )
总是大于0,正确的有( )A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(﹣2,0)、C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
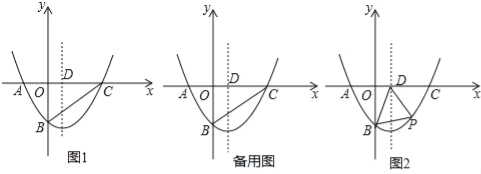
(1)求该二次函数的解析式;
(2)如图1,连结BC,在线段BC上是否存在点E,使得△CDE为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)如图2,若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB,PD,BD,求△BDP面积的最大值及此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南方某地突降暴雨,造成山洪爆发,导致一条重要公路损毁严重,某部工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的
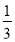 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.(1)按原计划完成总任务的
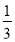 时,已抢修道路 米;
时,已抢修道路 米;(2)求原计划每小时抢修道路多少米?
相关试题

