【题目】解方程:
①![]() (直接开平方法)
(直接开平方法)
②![]() (用配方法)
(用配方法)
③![]() (用因式分解法)
(用因式分解法)
④![]()
⑤![]()
⑥![]()
⑦![]()
⑧(x-2)(x-5)=-2
参考答案:
【答案】(1) x1=2,x2=-1;(2)x1=1, x2=-4;(3)x1=-2, x2=4; (4)x1=-4,x2=1;(5)x1=x2=1;(6)x1=1, x2=-2;(7)x1=![]() x2=
x2=![]() (8)x1=3, x2=4
(8)x1=3, x2=4
【解析】试题分析:①②③根据要求的方法解方程即可;④可运用因式分解法解方程;⑤整理后运用直接开平方法解方程;⑥整理后运用因式分解法解方程;⑦运用公式法解方程;⑧整理后运用因式分解法解方程.
试题解析:
①、2x-1=±3,∴x1=2,x2=-1;
②、![]() ,∴x+
,∴x+![]() =±
=±![]() ,∴x1=1, x2=-4
,∴x1=1, x2=-4
③ (x+2)(x-4)=0,∴x1=-2, x2=4;
④![]() ∴x1=-4,x2=1
∴x1=-4,x2=1
⑤、x2+2x+1-4x=0 x2-2x+1=0 (x-1)2=0 ∴x1=x2=1
⑥、x2+x-2=0 (x-1)(x+2)=0 ∴x1=1, x2=-2
⑦,2x2-10x-3=0 ![]() ∴x1=
∴x1=![]() x2=
x2=![]()
⑧x2-7x+12=0,(x-3)(x-4)=0, ∴x1=3, x2=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B,顶点为C,将抛物线在A,C,B之间的部分记为图象E(A,B两点除外).
(1)求抛物线的顶点坐标.
(2)AB=6时,经过点C的直线y=kx+b(k≠0)与图象E有两个交点,结合函数的图象,求k的取值范围.
(3)若横、纵坐标都是整数的点叫整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,C,B之间的图象E与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
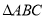 中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以
中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以 cm/s(
cm/s( >0且
>0且 )的速度从C点出发在线段CA上运动,设运动时间为
)的速度从C点出发在线段CA上运动,设运动时间为 秒。
秒。(1)若AB=AC,P在线段BC上,求当
 为何值时,能够使
为何值时,能够使 和
和 全等?
全等?(2)若
 ,求出发几秒后,
,求出发几秒后,  为直角三角形?
为直角三角形?(3)若
 ,当
,当 的度数为多少时,
的度数为多少时,  为等腰三角形?(请直接写出答案,不必写出过程)
为等腰三角形?(请直接写出答案,不必写出过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…依此类推,移动5次后该点对应的数为 , 这样移动10次后该点到原点的距离为a,则|a|= .
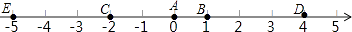
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)6xy2-9x2y-y3; (2)(p-4)(p+1)+3p.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经知道,有一个内角是直角的三角形是直角三角形.其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家已发现在一个直角三角形中,两个直角边边长的平方和等于斜边长的平方.如果设直角三角形的两条直角边长度分别是
 和
和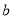 ,斜边长度是
,斜边长度是 ,那么可以用数学语言表达:
,那么可以用数学语言表达:  .
.
(1)在图②,若
 ,
,  ,则
,则 ;
;(2)观察图②,利用面积与代数恒等式的关系,试说明
 的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长.
相关试题

