【题目】我们已经知道,有一个内角是直角的三角形是直角三角形.其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家已发现在一个直角三角形中,两个直角边边长的平方和等于斜边长的平方.如果设直角三角形的两条直角边长度分别是![]() 和
和![]() ,斜边长度是
,斜边长度是![]() ,那么可以用数学语言表达:
,那么可以用数学语言表达: ![]() .
.

(1)在图②,若![]() ,
, ![]() ,则
,则![]() ;
;
(2)观察图②,利用面积与代数恒等式的关系,试说明![]() 的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长.
参考答案:
【答案】(1)12; (2)答案见解析;(3)5
【解析】试题分析:
(1)利用题中所给公式: ![]() ,代入
,代入![]() 即可解出
即可解出![]() 的值;
的值;
(2)先用“梯形面积计算公式”计算出图②的面积,再分别计算图②中三个三角形的面积并相加得到图②的面积,利用两次所求面积相等得到等式,把等式变形即可得到公式: ![]() ;
;
(3)由矩形和折叠的性质可得:AF=AD=BC=10,DC=AB=8,EF=DE;在Rt△ABF中,由题中所给结论可计算出BF的长,从而可得FC的长;设EF= ![]() ,则DE=
,则DE= ![]() ,EC=
,EC= ![]() ,这样在Rt△EFC中,由题中所给结论可得关于
,这样在Rt△EFC中,由题中所给结论可得关于![]() 的方程,解方程即可求得EF的长.
的方程,解方程即可求得EF的长.

试题解析:
(1)∵![]() ,代入
,代入![]() ,
,
∴![]() ;
;
(2)∵图①的面积=![]() =
=![]() ,
,
图①的面积=S梯形ABCD=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
即![]() .
.
(3)由四边形ABCD是矩形和折叠的性质可得, ![]() ,
, ![]() ,EF=DE,
,EF=DE,
由题意可得:在![]() ,即
,即![]() ,解得:
,解得: ![]() ,
,
又∵![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,
,
∵在Rt△ECF中, ![]() ,
,
∴![]() ,
,
解得 ![]() ,即
,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
①
 (直接开平方法)
(直接开平方法)②
 (用配方法)
(用配方法)③
 (用因式分解法)
(用因式分解法)④

⑤

⑥

⑦

⑧(x-2)(x-5)=-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)6xy2-9x2y-y3; (2)(p-4)(p+1)+3p.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图抛物线
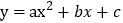 与
与 轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与
轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与 轴交于点E,CD⊥DE于D,现有下列结论:① a<0, ② b<0, ③
轴交于点E,CD⊥DE于D,现有下列结论:① a<0, ② b<0, ③ 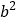 -4ac>0, ④ AE+CD=4,下列选项中选出的结论完全正确的是 .
-4ac>0, ④ AE+CD=4,下列选项中选出的结论完全正确的是 . 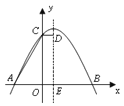
A. ①②③ B. ①②④ C. ①③④ D. ①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】用边长相等的正三角形和正六边形地砖拼地板,在每个顶点周围有a块正三角形和b块正六边形的地砖(ab≠0),则a-b的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当∠COE=40°时,求∠AOB的度数.
解:∵OE是∠COB的平分线,
∴∠COB=________(理由:________).
∵∠COE=40°,
∴________.
∵∠AOC=________,
∴∠AOB=∠AOC+________=110°.
相关试题

