【题目】【探索新知】
已知平面上有n(n为大于或等于2的正整数)个点A1 , A2 , A3 , …An , 从第1个点A1开始沿直线滑动到另一个点,且同时满足以下三个条件:①每次滑动的距离都尽可能最大;②n次滑动将每个点全部到达一次;③滑动n次后必须回到第1个点A1 , 我们称此滑动为“完美运动”,且称所有点为“完美运动”的滑动点,记完成n个点的“完美运动”的路程之和为Sn .
(1)如图1,滑动点是边长为a的等边三角形三个顶点,此时S3=;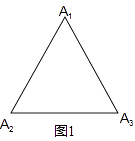
(2)如图2,滑动点是边长为a,对角线(线段A1A2、A2A4)长为b的正方形四个顶点,此时S4= .
【深入研究】
现有n个点恰好在同一直线上,相邻两点距离都为1,
(3)如图3,当n=3时,直线上的点分别为A1、A2、A3 .
为了完成“完美运动”,滑动的步骤给出如图4所示的两种方法:
方法1:A1→A3→A2→A1 , 方法2:A1→A2→A3→A1 .
①其中正确的方法为 .
A.方法1 B.方法2 C.方法1和方法2
②完成此“完美运动”的S3= . 

(4)当n分别取4,5时,对应的S4= , S5=
(5)若直线上有n个点,请用含n的代数式表示Sn .
参考答案:
【答案】
(1)3a
(2)2a+2b
(3)A;4
(4)8;12
(5)
解:n 为奇数时:Sn=n﹣1+n﹣2+…+1+ ![]() ﹣1=
﹣1= ![]() ;
;
n 为偶数时:Sn=n﹣1+n﹣2+…+1+ ![]() =
= ![]()
【解析】解:(1)如图1,∵滑动点是边长为a的等边三角形三个顶点,
∴S3=3a,
所以答案是:3a;(2)如图2,∵滑动点是边长为a,对角线长为b的正方形四个顶点,
∴S4=2a+2b,
所以答案是:2a+2b;(3)如图4,①∵方法2 是错的,不满足第①个条件,每一次距离要是最大的,
∴方法1正确,
故选A;②如图3,S3=2+1+1=4,
所以答案是:4;(4)根据条件:①每次滑动的距离都尽可能最大;②n次滑动将每个点全部到达一次;③滑动n次后必须回到第1个点A1 , 可得:
S4=3+2+1+2=8,
S5=4+3+2+1+2=12,
所以答案是:8,12;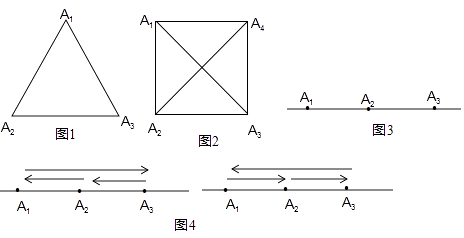
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)一个数的绝对值是指在数轴上表示这个数的点到的距离;
(2)若|a|=﹣a,则a0;
(3)有理数a、b在数轴上的位置如图所示,请化简|a|+|b|+|a+b|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一张长方形纸条上画一条数轴.

(1)若折叠纸条,数轴上表示﹣3的点与表示1的点重合,则折痕与数轴的交点表示的数为;
(2)若经过某次折叠后,该数轴上的两个数a和b表示的点恰好重合,则折痕与数轴的交点表示的数为(用含a,b的代数式表示);
(3)若将此纸条沿虚线处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折n次后,再将其展开,请分别求出最左端的折痕和最右端的折痕与数轴的交点表示的数.(用含n的代数式表示) -
科目: 来源: 题型:
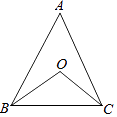
查看答案和解析>>【题目】如图,△ABC中,∠A=α°,BO,CO分别是∠ABC,∠ACB的平分线,则∠BOC的度数是( )
A.2α°
B.(α+60)°
C.(α+90)°
D.( α+90)°
α+90)° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=
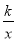 的图象上,则k的值为__.
的图象上,则k的值为__.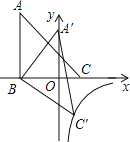
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3a2b3÷ a3b
a3b  ab3
ab3
(2)(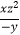 )3(
)3( 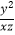 )4÷(
)4÷( 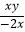 )3 .
)3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的情境对话,然后解答问题

(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt
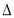 ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt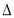 ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
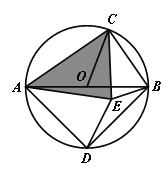
求证:
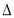 ACE是奇异三角形;
ACE是奇异三角形;当
 ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数.
相关试题

