【题目】阅读下面的情境对话,然后解答问题

(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt![]() ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt![]() ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
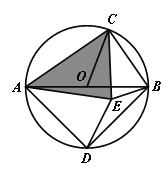
求证:![]() ACE是奇异三角形;
ACE是奇异三角形;
当![]() ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数.
参考答案:
【答案】解:(1)真命题
(2)在Rt![]() ABC 中a2+b2= c2,
ABC 中a2+b2= c2,
∵c>b>a>0
∴2c2>a2+b2,2a2<c2+b2
∴若Rt![]() ABC是奇异三角形,一定有2b2=c2+ a2
ABC是奇异三角形,一定有2b2=c2+ a2
∴2b2=a2+(a2+b2)
∴b2=2a2 得:b=![]() a
a
∵c2=b2+ a2=3a2
∴c=![]()
∴a:b: c=![]()
(3)∵AB是⊙O的直径ACBADB=90°
在Rt![]() ABC 中,AC2+BC2=AB2
ABC 中,AC2+BC2=AB2
在Rt![]() ADB 中,AD2+BD2=AB2
ADB 中,AD2+BD2=AB2
∵点D是半圆的中点
∴=
∴AD=BD
∴AB2=AD2+BD2=2AD2
∴AC2+CB2=2AD2
又∵CB=CE,AE=AD
∴AC2=CE2=2AE2
∴![]() ACE是奇异三角形
ACE是奇异三角形
由可得![]() ACE是奇异三角形
ACE是奇异三角形
∴AC2=CE2=2AE2
当![]() ACE是直角三角形时
ACE是直角三角形时

【解析】(1)根据“奇异三角形”的定义与等边三角形的性质,求证即可;
(2)根据勾股定理与奇异三角形的性质,可得a2+b2=c2与a2+c2=2b2,用a表示出b与c,即可求得答案;
(3)①AB是⊙O的直径,即可求得∠ACB=∠ADB=90°,然后利用勾股定理与圆的性质即可证得;
②利用(2)中的结论,分别从AC:AE:CE=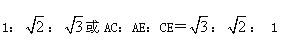 去分析,即可求得结果.
去分析,即可求得结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【探索新知】
已知平面上有n(n为大于或等于2的正整数)个点A1 , A2 , A3 , …An , 从第1个点A1开始沿直线滑动到另一个点,且同时满足以下三个条件:①每次滑动的距离都尽可能最大;②n次滑动将每个点全部到达一次;③滑动n次后必须回到第1个点A1 , 我们称此滑动为“完美运动”,且称所有点为“完美运动”的滑动点,记完成n个点的“完美运动”的路程之和为Sn .
(1)如图1,滑动点是边长为a的等边三角形三个顶点,此时S3=;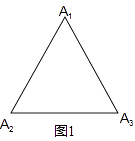
(2)如图2,滑动点是边长为a,对角线(线段A1A2、A2A4)长为b的正方形四个顶点,此时S4= .
【深入研究】
现有n个点恰好在同一直线上,相邻两点距离都为1,
(3)如图3,当n=3时,直线上的点分别为A1、A2、A3 .
为了完成“完美运动”,滑动的步骤给出如图4所示的两种方法:
方法1:A1→A3→A2→A1 , 方法2:A1→A2→A3→A1 .
①其中正确的方法为 .
A.方法1 B.方法2 C.方法1和方法2
②完成此“完美运动”的S3= .

(4)当n分别取4,5时,对应的S4= , S5=
(5)若直线上有n个点,请用含n的代数式表示Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=
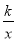 的图象上,则k的值为__.
的图象上,则k的值为__.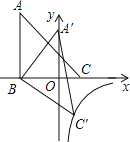
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3a2b3÷ a3b
a3b  ab3
ab3
(2)(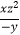 )3(
)3( 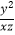 )4÷(
)4÷( 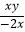 )3 .
)3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)).
问题:
(1)求∠ABC的度数;
(2)求证:△AEB≌△ADC;
(3)△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).
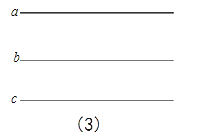
(4)如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.
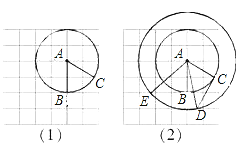
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)2+(﹣3)+(﹣6)+8
(2)1﹣(﹣4)÷22×
(3)( ﹣
﹣  +
+  )÷(﹣
)÷(﹣  )
)
(4)﹣12×8﹣8×( )3+4÷
)3+4÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣4x+m﹣1=0有两个相等的实数根,求m的值及方程的根.
相关试题

