搜索
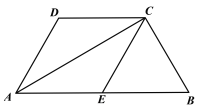
【题目】已知，四边形ABCD中，AB∥CD，AB=2CD，E为AB的中点，AC为对角线，AC⊥BC.
（1）求证：四边形AECD是菱形.
（2）若∠DAE=60°，AE=2，求菱形AECD的面积.
参考答案：
【答案】（1）见解析；（2）
【解析】(1)先证AE=CD，AE∥CD，得四边形AECD是平行四边形，再证CE=AE ，得
平行四边形AECD是菱形；
（2）过点C作CF⊥EB交EB于点F. 先求EF，再根据勾股定理求CF，再根据平行四边形面积公式可求出四边形面积.
（1）∵E为AB的中点
∴AB=2AE
∵AB=2CD
∴AE=CD
又∵AB∥CD
∴AE∥CD
∴四边形AECD是平行四边形
∵AC⊥BC
∴∠ACB=90°
又∵E为AB的中点
∴
,
∴CE=AE
平行四边形AECD是菱形
（2）过点C作CF⊥EB交EB于点F.
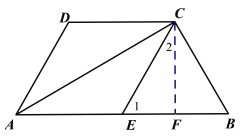
∵四边形AECD是菱形
∴AD∥EC，AE=CE
∴∠DAE=∠1
∵∠DAE=60°，AE=2
∴∠1=60°，CE=2
∵CF⊥EB
∴∠CFE=90°
∴∠1+∠2=90°
∴∠2=30°
∴
，
∴
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知整数a1，a2，a3，a4，…满足下列条件：a1=0，a2=﹣|a1+1|，a3=﹣|a2+2|，a4=﹣|a3+3|，……以此类推，则a2018的值为（ ）
A. ﹣1007 B. ﹣1008 C. ﹣1009 D. ﹣2018
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形OABC与正方形ODEF是位似图形，点O为位似中心，相似比为1：
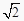，点A的坐标为（0，1），则点E的坐标是（ ） 
A.（-1.4，-1.4）
B.（1.4，1.4）
C.（- ，- ）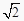
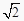D.（ ， ） -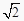
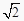科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC的三个顶点的坐标分别为A（-1，2）、B（-3，0）、C（0，0）
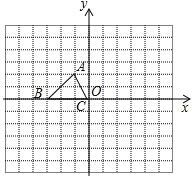
（1）请直接写出点A关于x轴对称的点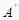
的坐标；
（2）以C为位似中心，在x轴下方作△ABC的位似图形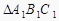
，使放大前后位似比为1：2，请画出图形，并求出 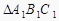的面积； -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，D为BC中点，BE、CF与射线AE分别相交于点E、F（射线AE不经过点D）.
（1）如图①，当BE∥CF时，连接ED并延长交CF于点H. 求证：四边形BECH是平行四边形；
（2）如图②，当BE⊥AE于点E，CF⊥AE于点F时，分别取AB、AC的中点M、N，连接ME、MD、NF、ND. 求证：∠EMD=∠FND.
图① 图②
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，C是线段AB的中点．
（1）若点D在CB上，且DB=2cm，AD=8cm，求线段CD的长度；
（2）若将（1）中的“点D在CB上”改为“点D在CB的延长线上”，其它条件不变，请画出相应的示意图，并求出此时线段CD的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于点G，若△CEF的面积为12cm2，则S△DGF的值为（ ）
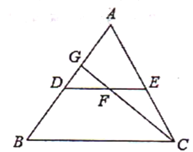
A．4cm2 B．6cm2 C．8cm2 D．9cm2
相关试题
