【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为( )
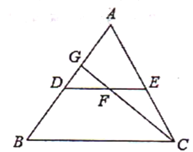
A.4cm2 B.6cm2 C.8cm2 D.9cm2
参考答案:
【答案】A
【解析】
试题分析:取CG的中点H,连接EH,根据三角形的中位线定理可得EH∥AD,再根据两直线平行,内错角相等可得∠GDF=∠HEF,然后利用“角边角”证明△DFG和△EFH全等,根据全等三角形对应边相等可得FG=FH,全等三角形的面积相等可得S△EFH=S△DGF,再求出FC=3FH,再根据等高的三角形的面积比等于底边的比求出两三角形的面积的比,从而得解.
解:如图,取CG的中点H,连接EH,
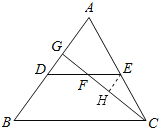
∵E是AC的中点,
∴EH是△ACG的中位线,
∴EH∥AD,
∴∠GDF=∠HEF,
∵F是DE的中点,
∴DF=EF,
在△DFG和△EFH中,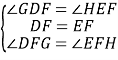 ,
,
∴△DFG≌△EFH(ASA),
∴FG=FH,S△EFH=S△DGF,
又∵FC=FH+HC=FH+GH=FH+FG+FH=3FH,
∴S△CEF=3S△EFH,
∴S△CEF=3S△DGF,
∴S△DGF=![]() ×12=4(cm2).
×12=4(cm2).
故选:A.
-
科目: 来源: 题型:
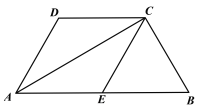
查看答案和解析>>【题目】已知,四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,AC为对角线,AC⊥BC.
(1)求证:四边形AECD是菱形.
(2)若∠DAE=60°,AE=2,求菱形AECD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,D为BC中点,BE、CF与射线AE分别相交于点E、F(射线AE不经过点D).
(1)如图①,当BE∥CF时,连接ED并延长交CF于点H. 求证:四边形BECH是平行四边形;
(2)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND. 求证:∠EMD=∠FND.


图① 图②
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C是线段AB的中点.
(1)若点D在CB上,且DB=2cm,AD=8cm,求线段CD的长度;

(2)若将(1)中的“点D在CB上”改为“点D在CB的延长线上”,其它条件不变,请画出相应的示意图,并求出此时线段CD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,
(1)问直线EF与AB有怎样的位置关系?加以证明;
(2)若∠CEF=70°,求∠ACB的度数.
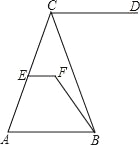
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC , AB=12,AC=15,D为AB上一点,且AD=
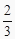 AB , 在AC上取一点E , 使以A、D、E为顶点的三角形与ABC相似,则AE等于( )
AB , 在AC上取一点E , 使以A、D、E为顶点的三角形与ABC相似,则AE等于( ) 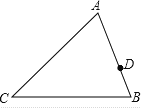
A.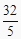
B.10
C.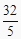 或10
或10
D.以上答案都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
相关试题

