【题目】在△ABC中,D为BC中点,BE、CF与射线AE分别相交于点E、F(射线AE不经过点D).
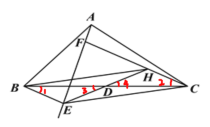
(1)如图①,当BE∥CF时,连接ED并延长交CF于点H. 求证:四边形BECH是平行四边形;
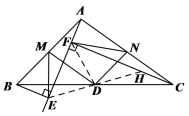
(2)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND. 求证:∠EMD=∠FND.


图① 图②
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)根据ASA证明△BDE≌△CDH.得ED=HD.又BD=CD,可得四边形BECH是平行四边形.
(2)连接FD、ED,延长ED交CF于点H,根据(1)可知ED=HD.可得ED=FD. 在Rt△AEB中,M是斜边AB中点,故![]() ,同理
,同理![]() .故ME=DN 同理,MD=NF. 由SSS证△MED≌△NDF.所以∠EMD=∠FND.
.故ME=DN 同理,MD=NF. 由SSS证△MED≌△NDF.所以∠EMD=∠FND.
证明:(1)∵D为BC中点,
∴BD=CD.
∵BE∥CF,
∴∠1=∠2.
又∵∠3=∠4,
∴△BDE≌△CDH.
∴ED=HD.
∴四边形BECH是平行四边形.
(2)连接FD、ED,延长ED交CF于点H,
∵BE⊥AE,CF⊥AE,
∴BE∥CF.
根据(1)可知ED=HD.
又∵CF⊥AE,
∴ED=FD.
∵Rt△AEB中,M是斜边AB中点,
∴![]() ,
,
∵△ABC中,D、N分别是BC、AC中点,
∴![]() .
.
∴ME=DN
同理,MD=NF.
∴△MED≌△NDF.
∴∠EMD=∠FND.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:
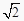 ,点A的坐标为(0,1),则点E的坐标是( )
,点A的坐标为(0,1),则点E的坐标是( ) 
A.(-1.4,-1.4)
B.(1.4,1.4)
C.(-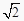 ,-
,- 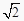 )
)
D.(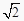 ,
, 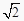 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0)
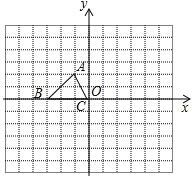
(1)请直接写出点A关于x轴对称的点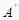 的坐标;
的坐标;
(2)以C为位似中心,在x轴下方作△ABC的位似图形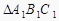 ,使放大前后位似比为1:2,请画出图形,并求出
,使放大前后位似比为1:2,请画出图形,并求出 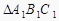 的面积;
的面积; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,AC为对角线,AC⊥BC.
(1)求证:四边形AECD是菱形.
(2)若∠DAE=60°,AE=2,求菱形AECD的面积.
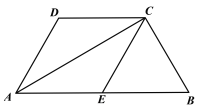
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C是线段AB的中点.
(1)若点D在CB上,且DB=2cm,AD=8cm,求线段CD的长度;

(2)若将(1)中的“点D在CB上”改为“点D在CB的延长线上”,其它条件不变,请画出相应的示意图,并求出此时线段CD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为( )
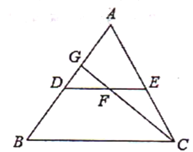
A.4cm2 B.6cm2 C.8cm2 D.9cm2
-
科目: 来源: 题型:
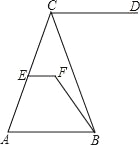
查看答案和解析>>【题目】如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,
(1)问直线EF与AB有怎样的位置关系?加以证明;
(2)若∠CEF=70°,求∠ACB的度数.
相关试题

