【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
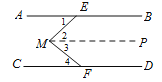
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).

参考答案:
【答案】(1)∠EMF=∠AEM+∠MFC,∠AEM+∠EMF+∠MFC=360°(2)第一图数量关系:∠EMN+∠MNF-∠AEM-∠NFC=180°.第二图数量关系:∠EMN-∠MNF+∠AEM+∠NFC=180°.
【解析】试题分析:(1)分点M在EF的左侧和右侧两种情况,当点M在EF的左侧时,如图,∠EMF=∠AEM+∠MFC,过点M作MP∥AB,可得AB∥CD∥MP, 根据平行线的性质可得∠4=∠3, ∠1=∠2,即可证得∠EMF=∠AEM+∠MFC;当点M在EF的右侧时,类比左侧的方法即可证得∠AEM+∠EMF+∠MFC=360°;(2)类比(1)的方法作平行线,利用平行线的性质即可解决.
试题解析:
(1)∠EMF=∠AEM+∠MFC.
证明:过点M作MP∥AB.
∵AB∥CD,
∴MP∥CD.
∴∠4=∠3.
∵MP∥AB,
∴∠1=∠2.
∵∠EMF=∠2+∠3,
∴∠EMF=∠1+∠4.
∴∠EMF=∠AEM+∠MFC.
∠AEM+∠EMF+∠MFC=360°
证明:过点M作MQ∥AB.
∵AB∥CD,
∴MQ∥CD.
∴∠CFM+∠1=180°.
∵MQ∥AB,
∴∠AEM+∠2=180°.
∴∠CFM+∠1+∠AEM+∠2=360°
∵∠EMF=∠1+∠2
∴∠AEM+∠EMF+∠MFC=360°.

(2)第一图数量关系:∠EMN+∠MNF-∠AEM-∠NFC=180°.
第二图数量关系:∠EMN-∠MNF+∠AEM+∠NFC=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并填空: 在体育比赛中,我们常常会遇到计算比赛场次的问题,这时我们可以借助数线段的方法来计算.比如在一个小组中有 4 个队,进行单循环比赛,我们要计算总的比赛场次,我们就 设这四个队分别为 A、B、C、D,并把它们标在同一条线段上,如下图:
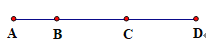
因为单循环比赛就是每两个队之间都要比赛一场,这就相当于,在上述图形中四个点连接线段,按一定规律得到的线段有:
AB,AC,AD…………3 条
BC,BD………………2 条
CD……………………1 条
总的线段条数是 3+2+1=6
所以可知 4 个队进行单循环比赛共比赛六场.
(1).类比上述想法,若一个小组有 6 个队,进行单循环比赛,则总的比赛场次是_____
(2).类比上述想法,若一个小组有 n 个队,进行单循环比赛,则总的比赛场次是_____
(3).我们知道 2006 年世界杯共有 32 支代表队参加比赛,共分成 8 个小组,每组 4 个 代表队.第一阶段每个小组进行单循环比赛.则第一阶段共 需 要 进 行_______ 场比赛.
(4).若分成 m 个小组,每个小组有 n 个队,第一阶段每个小组进行单循环比赛.则第 一阶段共需要进行_____________场比赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,…….照此规律,点P第100次跳动至点P100的坐标是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,则下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有四对全等三角形.其中正确结论的个数是( )
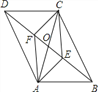
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选两个,并选择你认为适当的方法解这个方程.
①
 ②
② ③
③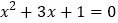 ④
④
我选择第 个方程。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,BC、AD是⊙O的切线,切点分别为B、A,过点O作EC⊥OD,EC交BC于点C,交AD于点E.

(1)求证:CE是⊙O的切线;
(2)若AE=1,AD=3,求阴影部分的面积.(结果保留π)
相关试题

