【题目】解方程:
我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选两个,并选择你认为适当的方法解这个方程.
①![]() ②
②![]() ③
③![]() ④
④![]()
我选择第 个方程。
参考答案:
【答案】①![]() ②
②![]() ③
③![]() ④
④![]()
【解析】试题分析:①此方程利用公式法解比较方便;②此方程利用因式分解法解比较方便;③此方程利用公式法解比较方便;④此方程利用因式分解法解比较方便.
试题解析:
我选第①个方程,解法如下:
x2-4x-1=0,
这里a=1,b=-4,c=-1,
∵△=16+4=20,
∴x=![]() =2±
=2±![]() ,
,
则x1=2+![]() ,x2=2-
,x2=2-![]() ;
;
我选第②个方程,解法如下:
x(2x+1)=8x-3,
整理得:2x2-7x+3=0,
分解因式得:(2x-1)(x-3)=0,
可得2x-1=0或x-3=0,
解得:x1=![]() ,x2=3;
,x2=3;
我选第③个方程,解法如下:
x2+3x+1=0,
这里a=1,b=3,c=1,
∵△=9-4=5,
∴x=![]() ,
,
则x1=![]() ,x2=
,x2=![]() ;
;
我选第④个方程,解法如下:
x2-9=4(x-3),
变形得,(x+3)(x-3)-4(x-3)=0,
因式分解得,(x-3)(x+3-4)=0,
∴x-3=0或x+3-4=0,
∴x1=3,x2=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,则下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有四对全等三角形.其中正确结论的个数是( )
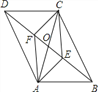
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,BC、AD是⊙O的切线,切点分别为B、A,过点O作EC⊥OD,EC交BC于点C,交AD于点E.

(1)求证:CE是⊙O的切线;
(2)若AE=1,AD=3,求阴影部分的面积.(结果保留π) -
科目: 来源: 题型:
查看答案和解析>>【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早
 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题: 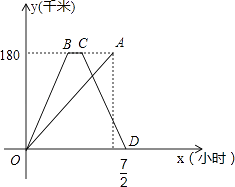
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?直接写出答案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形ABCD中,对角线AC、BD交于点O,动点P在线段BC上(不含点B),∠BPE=
 ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)如图②,当点P与点C重合时,求证:△BOG≌△POE;
(2)通过观察、测量、猜想: = , 并结合图①证明你的猜想;
= , 并结合图①证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图②),若∠ACB=a,直接写出 的值,为 . (用含a的式子表示)
的值,为 . (用含a的式子表示)
相关试题

