【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() -1来表示
-1来表示![]() 的小数部分,事实上,小明的表示方法是有道理的,因为
的小数部分,事实上,小明的表示方法是有道理的,因为![]() <
<![]() <
<![]() ,所以
,所以![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.请据此解答:
的整数部分是1,将这个数减去其整数部分,差就是小数部分.请据此解答:
(1)![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)若设2+![]() 的整数部分为x,小数部分为y,求(y-x)2的值.
的整数部分为x,小数部分为y,求(y-x)2的值.
参考答案:
【答案】(1)3,![]() ;(2)a+b-
;(2)a+b-![]() =4;(3)(y-x)2=19-
=4;(3)(y-x)2=19-![]() .
.
【解析】
(1)由3<![]() <4可得答案;
<4可得答案;
(2)由2<![]() <3知a=
<3知a=![]() -2,由6<
-2,由6<![]() <7知b=6,据此求解可得;
<7知b=6,据此求解可得;
(3)由1<![]() <2知3<2+
<2知3<2+![]() <4,据此得出x、y的值代入计算可得.
<4,据此得出x、y的值代入计算可得.
(1)(1)∵3<![]() <4,
<4,
∴![]() 的整数部分是3,小数部分是
的整数部分是3,小数部分是![]() -3;
-3;
故答案为:3;![]() -3.
-3.
(2)∵2<![]() <3, a=
<3, a=![]() -2,
-2,
∵6<![]() <7,∴b=6
<7,∴b=6
∴a+b-![]() =
=![]() -2+6-
-2+6-![]() =4
=4
(3)∵1<![]() <2,∴3<2+
<2,∴3<2+![]() <4,
<4,
∴2+![]() 的整数部分为x=3,小数部分为y=2+
的整数部分为x=3,小数部分为y=2+![]() -3=
-3=![]() -1
-1
∴(y-x)2=(![]() -4)2=19-
-4)2=19-![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(3,0),B(0,1)

(1)将△ABC沿x轴的正方向平移t个单位,B、C两点的对应点B′、C′正好落在反比例函数y=
 的图象上.请直接写出C点的坐标和t,k的值;
的图象上.请直接写出C点的坐标和t,k的值;(2)有一个Rt△DEF,∠D=90°,∠E=60°,DE=2,将它放在直角坐标系中,使斜边EF在x轴上,直角顶点D在(1)中的反比例函数图象上,求点F的坐标;
(3)在(1)的条件下,问是否存在x轴上的点M和反比例函数y=
 图象上的点N,使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在,直接写出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
图象上的点N,使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在,直接写出所有满足条件的点M和点N的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划组织
 名师生租乘汽车外出研学一天,需租用大巴、中巴共
名师生租乘汽车外出研学一天,需租用大巴、中巴共 辆,且要求租用的车子不留空位也不超载,大巴每辆可乘坐
辆,且要求租用的车子不留空位也不超载,大巴每辆可乘坐 名乘客,中巴每辆可乘坐
名乘客,中巴每辆可乘坐 名乘客.
名乘客.(1)求该校应租用大巴、中巴各多少辆?(请用含
 的代数式表示)
的代数式表示)(2)若每辆大巴租金是
 元/天,中巴租金是
元/天,中巴租金是 元/天,若租金不能超过
元/天,若租金不能超过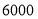 元,则应租用大巴、中巴各多少辆?
元,则应租用大巴、中巴各多少辆? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的一元二次方程
的一元二次方程 .
.(1)若此方程的一个根为1,求
 的值;
的值;(2)求证:不论
 取何实数,此方程都有两个不相等的实数根.
取何实数,此方程都有两个不相等的实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】利民商场经营某种品牌的T恤,购进时的单价是300元,根据市场调查:在一段时间内,销售单价是400元时,销售量是60件,销售单价每涨10元,销售量就减少1件.设这种T恤的销售单价为x元(x>400)时,销售量为y件、销售利润为W元.
(1)请分别用含x的代数式表示y和W(把结果填入下表):
销售单价(元)
x
销售量y(件)
销售利润W(元)
(2)该商场计划实现销售利润10000元,并尽可能增加销售量,那么x的值应当是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)用“=”、“>”、“<”填空
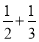
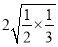 ; 6+3
; 6+3 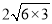 ;
;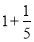
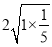 ;7+7
;7+7 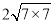 ;
;(2)由(1)中各式猜想a+b与
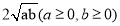 的大小,并说明理由.
的大小,并说明理由.(3)请利用上述结论解决下面问题:
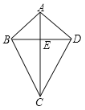
某同学在做一个面积为1800cm2,对角线互相垂直的四边形风筝时,求用来做对角线的竹条至少要多少厘米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为一个矩形纸片,AB=3,BC=2,动点P自D点出发沿DC方向运动至C点后停止,△ADP以直线AP为轴翻折,点D落在点D1的位置,设DP=x,△AD1P与原纸片重叠部分的面积为y.

(1)当x为何值时,直线AD1过点C?
(2)当x为何值时,直线AD1过BC的中点E?
(3)求出y与x的函数表达式.
相关试题

