【题目】如图,平面直角坐标系中,每个小正方形边长都是1.

(1)按要求作图: △ABC关于![]() 轴对称的图形△
轴对称的图形△![]() ;
;
(2)将点![]() 先向上平移
先向上平移![]() 个单位,再向右平移
个单位,再向右平移![]() 个单位得到点
个单位得到点![]() 的坐标为 ;
的坐标为 ;
(3)△![]() 的面积为 ;
的面积为 ;
(4)若![]() 为
为![]() 轴上一点,连接
轴上一点,连接![]()
![]() ,则△
,则△![]() 周长的最小值为 .
周长的最小值为 .
参考答案:
【答案】(1)见解析(2)(3,2)(3)![]() (4)5+
(4)5+![]()
【解析】
(1)根据关于y轴对称的性质画出△A1B1C1;
(2)根据点平移的坐标规律直接得出A2的坐标;
(3)用△ABC三个顶点所在网格线围成的矩形面积减去△ABC周围三个直角三角形的面积即可;
(4)找到点A关于x轴的对称点A3,连接A3B交x轴与点Q,此时△ABQ的周长最小.
解:(1)如图所示:
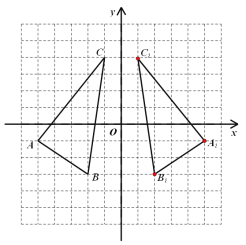 ;
;
(2)将点A先向上平移![]() 个单位,再向右平移
个单位,再向右平移![]() 个单位得到点
个单位得到点![]() 的坐标为
的坐标为![]() ;
;
(3)4×7-![]() ×4×5-
×4×5-![]() ×2×3-
×2×3-![]() ×1×7=
×1×7=![]() ;
;
(4)如图,作点A关于x轴的对称点A3,连接A3B交x轴与点Q,此时△ABQ的周长最小,
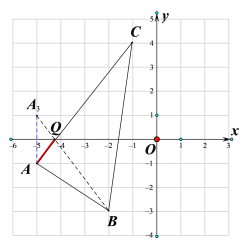
∴AQ+BQ=A3B=![]() =5,
=5,
AB=![]() =
=![]() ,
,
△ABQ的周长=5+![]() .
.
故答案为:(1)见解析;(2)(3,2);(3)![]() ;(4)5+
;(4)5+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克
1
2
3
4
5
6
7
8
9
…
销售额/元
2
4
6
8
10
12
14
16
18
…
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用
 表示橘子卖出的质量,
表示橘子卖出的质量, 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系, 与
与 之间的关系式为______.
之间的关系式为______.(4)当橘子的销售额是100元时,共卖出多少千克橘子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 是角平分线,
是角平分线, ,
,
(1)求
 的度数.
的度数.(2)过点
 作
作 边上的高
边上的高 , 垂足为
, 垂足为 ;求
;求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=4,BC=2,点P、E、F分别为边BC、AB、AC上的任意点,则PE+PF的最小值是_____.
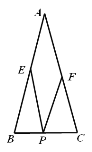
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
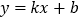 的图像经过点
的图像经过点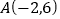 ,且与
,且与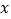 轴相交于点
轴相交于点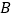 ,与正比例函数
,与正比例函数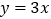 的图像交于点
的图像交于点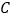 ,点
,点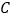 的横坐标为
的横坐标为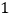 .
.(1)求
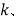
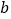 的值;
的值;(2)若点
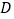 在
在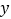 轴上,且满足
轴上,且满足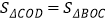 ,求点
,求点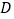 的坐标.
的坐标.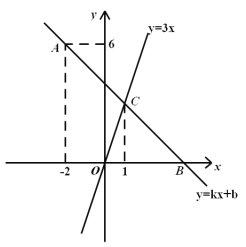
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.

(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在直线形的公路上由A向B行驶,M、N分别是位于公路AB两侧的两个学校,如图.
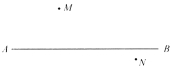
(1)汽车行驶时,会对公路两旁的学校都造成一定的影响,当汽车行驶到何处时,分别对两个学校影响最大?在图中标出来;
(2)当汽车从A向B行驶时,在哪一段上对两个学校影响越来越大?越来越小?对M学校影响逐渐减小而对N学校影响逐渐增大?
相关试题

