【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用![]() 表示橘子卖出的质量,
表示橘子卖出的质量,![]() 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系,![]() 与
与![]() 之间的关系式为______.
之间的关系式为______.
(4)当橘子的销售额是100元时,共卖出多少千克橘子?
参考答案:
【答案】(1)橘子卖出的质量与销售额之间的关系,橘子卖出的质量是自变量,销售额是因变量;(2)10;(3)![]() ;(4)共卖出50千克橘子.
;(4)共卖出50千克橘子.
【解析】
(1)根据表格第一列确定变量,再结合自变量和因变量的定义确定自变量与因变量;(2)根据表格解答即可;(3)根据表格可知单价,由单价×数量=总价即可得出y与x的关系式;(4)把y=100代入(3)中的关系式,即可求出销售橘子数量;
解:(1)橘子卖出的质量与销售额之间的关系,橘子卖出的质量是自变量,销售额是因变量;
(2)由表格可知:橘子卖出5千克时,销售额是10元;
故答案为:10
(3)由表格可知橘子的销售单价为2元/千克,
∴![]() .
.
故答案为:y=2x
(4)当![]() 时,
时,![]() .
.
答:此时共卖出50千克橘子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些相关的代数等式,这些等式可用于代数式的证明或求一些不规则图形的面积.
(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为
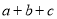 的正方形,若把这个大正方形的面积直接用边长表示,其面积是________;若把这个大正方形的面积用分割成的小正方形或小矩形的面积表示时,其面积是________;无论怎样表示,面积不变,所以,可得等式是________;并用多项式的乘法公式说明该等式成立;
的正方形,若把这个大正方形的面积直接用边长表示,其面积是________;若把这个大正方形的面积用分割成的小正方形或小矩形的面积表示时,其面积是________;无论怎样表示,面积不变,所以,可得等式是________;并用多项式的乘法公式说明该等式成立;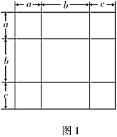
(2)已知三个数
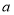 ,
,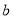 ,
,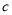 满足
满足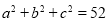 ,
,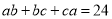 ,利用(1)中发现的结论可直接写出
,利用(1)中发现的结论可直接写出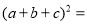 ________;
________;(3)如图2,是将两个边长分别为
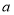 和
和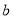 的正方形拼在一起,
的正方形拼在一起,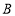 ,
,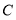 ,
,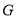 三点在同一直线上,连接
三点在同一直线上,连接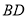 和
和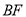 ,若两正方形的边长满足
,若两正方形的边长满足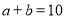 ,
,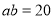 ,请求出阴影部分的面积.
,请求出阴影部分的面积.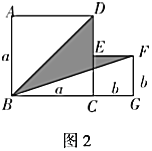
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中, ,
,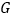 是
是 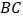 的中点.将
的中点.将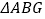 沿
沿 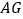 对折至
对折至 , 延长
, 延长 交
交  于点
于点 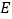 ,则
,则 的长是____.
的长是____.
-
科目: 来源: 题型:
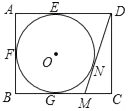
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )
A.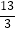
B.
C.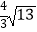
D.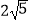
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 是角平分线,
是角平分线, ,
,
(1)求
 的度数.
的度数.(2)过点
 作
作 边上的高
边上的高 , 垂足为
, 垂足为 ;求
;求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=4,BC=2,点P、E、F分别为边BC、AB、AC上的任意点,则PE+PF的最小值是_____.
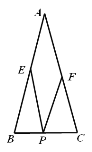
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,每个小正方形边长都是1.

(1)按要求作图: △ABC关于
 轴对称的图形△
轴对称的图形△ ;
; (2)将点
 先向上平移
先向上平移 个单位,再向右平移
个单位,再向右平移 个单位得到点
个单位得到点 的坐标为 ;
的坐标为 ; (3)△
 的面积为 ;
的面积为 ; (4)若
 为
为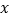 轴上一点,连接
轴上一点,连接
 ,则△
,则△ 周长的最小值为 .
周长的最小值为 .
相关试题

