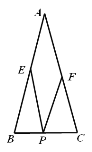
【题目】如图,在△ABC中,AB=AC=4,BC=2,点P、E、F分别为边BC、AB、AC上的任意点,则PE+PF的最小值是_____.
参考答案:
【答案】![]()
【解析】
当PE⊥AB,PF⊥AC时,PE+PF的值最小.
解:如图,作CG⊥AB于G,PH⊥CG于H,
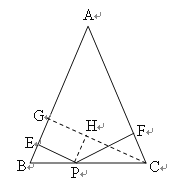
当PE⊥AB,PF⊥AC时,则∠EGH=GHP=∠PEG=90°,
∴四边形PEGH为矩形,
∴PE=HG,PH∥AB,
∴∠B=∠HPC,
∵AB=AC,
∴∠B=∠FCP,
∴∠HPC=∠FCP,
∵∠PHC=∠CFP=90°,PC=CP,
∴△PHC≌△CFP(AAS),
∴CH=PF
∴PE+PF=HG+CH=CG,
故此时PE+PF将取得最小值.
在Rt△ACG中,
∵AC=4,
∴CG2=AC2-AG2=42-AG2,
在Rt△BCG中,
∵BC=2,BG=AB-AG=4-AG,
∴CG2=BC2-BG2=22-(4-AG)2,
∴42-AG2=22-(4-AG)2,
∴AG=![]() ,
,
∴CG=![]() =
=![]() =
=![]() ,
,
∴PE+PF=![]() ,
,
即PE+PF的最小值为![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
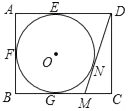
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )
A.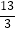
B.
C.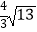
D.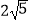
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克
1
2
3
4
5
6
7
8
9
…
销售额/元
2
4
6
8
10
12
14
16
18
…
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用
 表示橘子卖出的质量,
表示橘子卖出的质量, 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系, 与
与 之间的关系式为______.
之间的关系式为______.(4)当橘子的销售额是100元时,共卖出多少千克橘子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 是角平分线,
是角平分线, ,
,
(1)求
 的度数.
的度数.(2)过点
 作
作 边上的高
边上的高 , 垂足为
, 垂足为 ;求
;求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,每个小正方形边长都是1.

(1)按要求作图: △ABC关于
 轴对称的图形△
轴对称的图形△ ;
; (2)将点
 先向上平移
先向上平移 个单位,再向右平移
个单位,再向右平移 个单位得到点
个单位得到点 的坐标为 ;
的坐标为 ; (3)△
 的面积为 ;
的面积为 ; (4)若
 为
为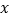 轴上一点,连接
轴上一点,连接
 ,则△
,则△ 周长的最小值为 .
周长的最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
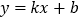 的图像经过点
的图像经过点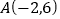 ,且与
,且与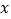 轴相交于点
轴相交于点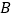 ,与正比例函数
,与正比例函数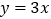 的图像交于点
的图像交于点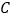 ,点
,点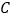 的横坐标为
的横坐标为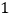 .
.(1)求
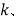
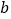 的值;
的值;(2)若点
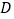 在
在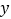 轴上,且满足
轴上,且满足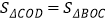 ,求点
,求点 的坐标.
的坐标.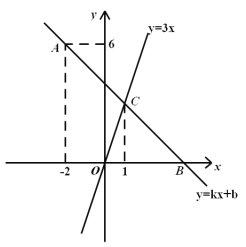
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.

(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.
相关试题

