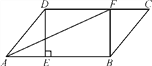
【题目】如图,在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据已知条件易证四边形BFDE是平行四边形,再证明∠DEB=90°即可得结论;(2)根据已知条件证明AD=DF,根据等腰三角形的性质可得∠DAF=∠DFA;再由AB∥CD,可得∠DFA=∠FAB.即可得∠DAF=∠FAB,结论得证.
试题解析:
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵CF=AE,
∴BE=DF.
又∵BE∥DF,
∴四边形BFDE为平行四边形.
∵DE⊥AB,
∴∠DEB=90°.
∴四边形BFDE是矩形.
(2)∵四边形BFDE是矩形,
∴∠BFD=90°.∴∠BFC=90°.
在Rt△BFC中,由勾股定理,得BC=![]() =
=![]() =10.
=10.
∴AD=BC=10.
又∵DF=10,
∴AD=DF.
∴∠DAF=∠DFA.
∵AB∥CD,
∴∠DFA=∠FAB.
∴∠DAF=∠FAB.
∴AF是∠DAB的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有三张分别标有1、2、3数字的卡片(卡片除数字外完全相同).
(1)从袋中任意抽取一张卡片,则抽出的是偶数的概率为 ;
(2)从袋中任意抽取二张卡片,求被抽取的两张卡片构成两位数是奇数的概率.
-
科目: 来源: 题型:
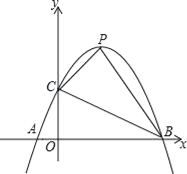
查看答案和解析>>【题目】已知,如图,抛物线y=﹣x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα﹣tanβ=2,OC2=OAOB.
(1)△ABC是否为直角三角形?若是,请给出证明;若不是,请说明理由;
(2)求抛物线的解析式;
(3)若抛物线的顶点为P,求四边形ABPC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m2+n2﹣2m+4n+5=0.则m﹣n=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数
1
2
3
4
5
小王
60
75
100
90
75
小李
70
90
100
80
80
根据上表解答下列问题:
(1)完成下表:
姓名
平均成绩(分)
中位数(分)
众数(分)
方差
小王
80
75
75
190
小李
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据从小到大排列为1,2,4,x,6,8.这组数据的中位数是5,那么这组数据的众数为( )
A. 4 B. 5 C. 5.5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.

相关试题

