【题目】在数轴上,数![]() 所对应的点与原点的距离叫做数
所对应的点与原点的距离叫做数![]() 的绝对值,记作
的绝对值,记作![]()
提出问题:(1)点![]() 所表示的数如图所示,则
所表示的数如图所示,则![]() 两点间的距离是 ,
两点间的距离是 ,![]() 两点间的距离是_____,
两点间的距离是_____,![]() 两点间的距离是 .
两点间的距离是 .
探究结论:(2)在数轴上,若![]() 两点对应的数分别是
两点对应的数分别是![]() ,则
,则![]() ____ (用含有
____ (用含有![]() 的式子表示).
的式子表示).
拓展应用:(3)请利用.上述结论,解决下列问题:
①![]() 和
和![]() 在数轴上对应的点之间的距离为
在数轴上对应的点之间的距离为
②![]()
③满足![]() 的未知数的值为
的未知数的值为

参考答案:
【答案】(1)![]() ;
;![]() ;
;![]() (2)
(2)![]() (3)①
(3)①![]() ②
②![]() ③2或-3
③2或-3
【解析】
(1)直接根据绝对值的定义求解即可;
(2)根据绝对值的定义求解即可;
(3)①根据(2)中的结论求解;
②根据绝对值的定义去绝对值符号后计算即可;
③x-1表示数轴上表示x的点与表示1的点之间的距离,x+2表示数轴上表示x的点与表示-2的点之间的距离,结合数轴即可求解.
(1)根据题意可得:
A表示-5,B表示![]() ,C表示3,D表示
,C表示3,D表示![]()
∴C、D两点间的距离是![]() ;
;
A、B两点间的距离是![]() ;
;
A、D两点间的距离是![]() .
.
故答案为:![]() ;
;![]() ;
;![]() .
.
(2)在数轴上,若![]() 两点对应的数分别是
两点对应的数分别是![]() ,则
,则![]()
![]()
故答案为:![]()
(3)①![]() 和
和![]() 在数轴上对应的点之间的距离为
在数轴上对应的点之间的距离为![]()
故答案为:![]()
②![]()
![]()
![]()
![]()
③根据题意得:![]() 即为数轴上表示x的点到1与-2的距离之和为5,而1-(-2)=3,故表示x的点不在1与-2含(1与-2)之间,故x>1或x<-2;
即为数轴上表示x的点到1与-2的距离之和为5,而1-(-2)=3,故表示x的点不在1与-2含(1与-2)之间,故x>1或x<-2;
当x>1时,x-1+x+2=5,x=2
当x<-2时,1-x-x-2=5,x=-3
故答案为:2或-3
-
科目: 来源: 题型:
查看答案和解析>>【题目】“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里,如果知道“远航”号沿东北方向航行,你能知道“海天”号沿哪个方向航行吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户承包荒山若干亩,种果树
 棵,今年水果总产量为
棵,今年水果总产量为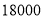 千克.目前有两种销售方式:一、此水果在市场上每千克售
千克.目前有两种销售方式:一、此水果在市场上每千克售 元,该农户将水果拉到市场出售平均每天出售
元,该农户将水果拉到市场出售平均每天出售 千克,需
千克,需 人帮忙,每人每天需付工资
人帮忙,每人每天需付工资 元,农用车运费及其他各项税费平均每天
元,农用车运费及其他各项税费平均每天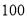 元.二、 直接在果园每千克售
元.二、 直接在果园每千克售 元
元 .
.(1)分别用
 表示两种方式出售水果的收入.
表示两种方式出售水果的收入.(2)若
 元,
元, 元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好?
元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,不能判断△ABC是直角三角形的是( )
A. a:b:c=3:4:5 B. ∠A:∠B:∠C=3:4:5
C. ∠A+∠B=∠C D. a:b:c=1:2:

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.
(1)求k的值;
(2)在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若点A在数轴上对应的数为
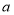 ,点B在数轴上对应的数为b,且
,点B在数轴上对应的数为b,且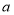 ,b满足
,b满足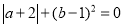
(1)求线段AB的长;
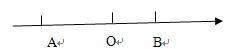
(2)点C在数轴上对应的数为x,且x是方程
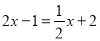 的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;
的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;(3)在(1)(2)条件下,点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB﹣BC的值是否随时间t的变化而改变?若变化,请说明理由;若不变,请求其常数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
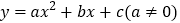 的对称轴为直线
的对称轴为直线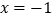 ,且抛物线与
,且抛物线与 轴交于
轴交于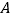 、
、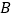 两点,与
两点,与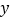 轴交于
轴交于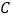 点,其中
点,其中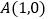 ,
,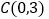 .
.
(1)若直线
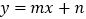 经过
经过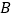 、
、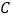 两点,求直线
两点,求直线 和抛物线的解析式;
和抛物线的解析式;(2)在抛物线的对称轴
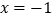 上找一点
上找一点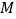 ,使点
,使点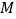 到点
到点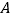 的距离与到点
的距离与到点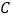 的距离之和最小,求出点
的距离之和最小,求出点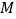 的坐标;
的坐标;(3)设点
 为抛物线的对称轴
为抛物线的对称轴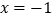 上的一个动点,求使
上的一个动点,求使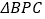 为直角三角形的点
为直角三角形的点 的坐标.
的坐标.
相关试题

