【题目】两组邻边分别相等的四边形我们称它为筝形,如图,在筝形ABCD中,AB=AD,BC=DC,AC,BD相交于点O.

(1)求证:①△ABC≌△ADC;②OB=OD,AC⊥BD;
(2)如果AC=6,BD=4,求筝形ABCD的面积.
参考答案:
【答案】(1)见解析;(2)12;
【解析】
(1)分别利用SSS,SAS求证△ABC≌△ADC,△ABO≌△ADO,从而得出OB=OD,AC⊥BD.
(2)筝形的面积公式可用△ABC的面积与△ACD的面积和求得.
(1)证明:①在△ABC和△ADC中,
AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADC(SSS).
②∵△ABC≌△ADC,
∴∠BAO=∠DAO.
∵AB=AD,∠BAO=∠DAO,OA=OA,
∴△ABO≌△ADO(SAS).
∴OB=OD,AC⊥BD.
(2)筝形ABCD的面积=△ABC的面积+△ACD的面积=![]() ×AC×BO+
×AC×BO+![]() ×AC×DO=
×AC×DO=![]() ×AC×(BO+DO)=
×AC×(BO+DO)=![]() ×AC×BD=
×AC×BD=![]() ×6×4=12.
×6×4=12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠CME+∠ABF=180°,MA平分∠CMN.若∠MNA=62°,求∠A的度数.根据提示将解题过程补充完整.
解:因为∠ABM+∠ABF=180°,
又因为∠CME+∠ABF=180°(已知),
所以∠ABM=∠CME
所以AB∥CD,理由:( )
所以∠CMN+( )=180°,
理由:(__________________________)
因为∠MNA=62°,
所以∠CMN=( )
因为MA平分∠CMN,
所以∠AMC=
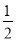 ∠CMN =( ).(角平分线的定义)
∠CMN =( ).(角平分线的定义)因为AB∥CD,
所以∠A=∠AMC=( )理由:(__________________________________)
-
科目: 来源: 题型:
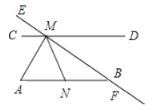
查看答案和解析>>【题目】如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
-
科目: 来源: 题型:
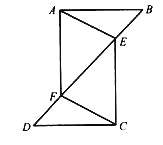
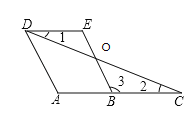
查看答案和解析>>【题目】已知:如图,AD∥BE,∠A=∠E,
(1)求证:∠1=∠2;
(2)若DC平分∠ADE,直接写出图中所有与∠1相等的角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B
 C
C D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
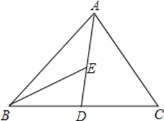
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
(1)若∠ABE=20°,∠BAD=45°,求∠BED的度数;
(2)画出△BED中BD边上的高;
(3)若△ABC的面积为80,BD=8,则点E到BC边的距离为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】早在1960年、中国登山队首次从珠穆朗玛北侧中国境内登上珠峰,近几十年,珠峰更是吸引了大批的登山爱好者,某日,登山运动员傅博准备从海拔7400米的3号营地登至海拔近7900米的4号营地,由于天气骤变,近6小时的攀爬过程中他不得不几次下撤躲避强高空风,记向上爬升的海拔高度为正数,向下撒退时下降的海拔高度为负数,傅博在这一天攀爬的海拔高度记录如下:(单位:米)+320、-55、+116、-20、+81、-43、+115.
(1)傳博能按原计划在这天登至4号营地吗?
(2)若在这一登山过程中,傅博所处位置的海拔高度上升或下降1米平均消耗8大卡的卡路里,则傅博这天消耗了多少卡路里?
(3)登山消耗的卡路里预估为:1千克身体重量(体重或负重)1天需要55~65(大于等于55,小于等于65)大卡的卡路里,海拔6000米以上会使卡路里消耗增加20%,登山协会约定海拔5000米以上运动员负重14千克,在(2)的条件下,请你估算傳博的体重范围.(精确到1千克)
相关试题

