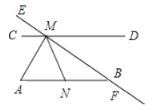
【题目】如图,∠CME+∠ABF=180°,MA平分∠CMN.若∠MNA=62°,求∠A的度数.根据提示将解题过程补充完整.
解:因为∠ABM+∠ABF=180°,
又因为∠CME+∠ABF=180°(已知),
所以∠ABM=∠CME
所以AB∥CD,理由:( )
所以∠CMN+( )=180°,
理由:(__________________________)
因为∠MNA=62°,
所以∠CMN=( )
因为MA平分∠CMN,
所以∠AMC=![]() ∠CMN =( ).(角平分线的定义)
∠CMN =( ).(角平分线的定义)
因为AB∥CD,
所以∠A=∠AMC=( )理由:(__________________________________)
参考答案:
【答案】同位角相等,两直线平行;∠MNA;两直线平行,同旁内角互补;118°;59°;59°;两直线平行,内错角相等
【解析】
根据同角的补角相等可得出∠ABM=∠CME,利用“同位角相等,两直线平行”可得出AB∥CD,由“两直线平行,同旁内角互补”及∠MNA =62°可求出∠CMN =118°,结合角平分线的定义可求出∠AMC的度数,再利用“两直线平行,内错角相等”即可求出∠A的度数.
解:因为∠ABM+∠ABF=180°,
又因为∠CME+∠ABF=180°(已知),
所以∠ABM=∠CME
所以AB∥CD,(同位角相等,两直线平行)
所以∠CMN+∠MNA=180°,(两直线平行,同旁内角互补)
因为∠MNA=62°,
所以∠CMN=118°,
因为MA平分∠CMN,
所以∠AMC=![]() ∠CMN =59°.(角平分线的定义)
∠CMN =59°.(角平分线的定义)
因为AB∥CD,
所以∠A=∠AMC=59°(两直线平行,内错角相等)
故答案为:同位角相等,两直线平行;∠MNA;两直线平行,同旁内角互补;118°;59°;59°;两直线平行,内错角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11分)如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于C点,且经过点(2,﹣3a),对称轴是直线x=1,顶点是M.
(1)求抛物线对应的函数表达式;
(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;
(4)当E是直线y=﹣x+3上任意一点时,(3)中的结论是否成立(请直接写出结论).

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
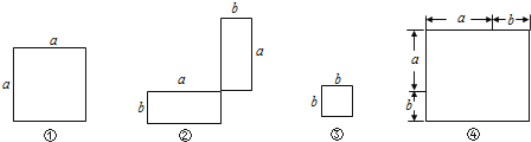
① ; ② ; ③ ; ④ .
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示: ;
(3)利用(2)的结论计算992+2×99×1+1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的中线, DE⊥AB于E, DF⊥AC于F, 且BE=CF, 求证:(1)AD是∠BAC的平分线;(2)AB=AC.

-
科目: 来源: 题型:
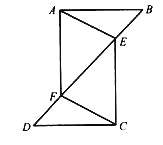
查看答案和解析>>【题目】如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
-
科目: 来源: 题型:
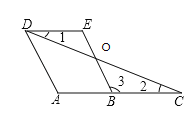
查看答案和解析>>【题目】已知:如图,AD∥BE,∠A=∠E,
(1)求证:∠1=∠2;
(2)若DC平分∠ADE,直接写出图中所有与∠1相等的角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两组邻边分别相等的四边形我们称它为筝形,如图,在筝形ABCD中,AB=AD,BC=DC,AC,BD相交于点O.

(1)求证:①△ABC≌△ADC;②OB=OD,AC⊥BD;
(2)如果AC=6,BD=4,求筝形ABCD的面积.
相关试题

