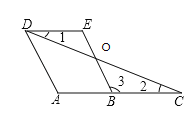
【题目】已知:如图,AD∥BE,∠A=∠E,
(1)求证:∠1=∠2;
(2)若DC平分∠ADE,直接写出图中所有与∠1相等的角.
参考答案:
【答案】(1)见解析;(2)∠ADC、∠BOC、∠DOE、∠2.
【解析】
(1)由AD与BE平行,利用两直线平行同位角相等得到一对角相等,再由已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到DE与AC平行,利用两直线平行内错角相等即可得证;
(2)根据角平分线的定义和平行线的性质以及对顶角可得结论.
解:(1)证明:∵AD∥BE,
∴∠A=∠3,
∵∠A=∠E,
∴∠3=∠E,
∴DE∥AB,
∴∠1=∠2;
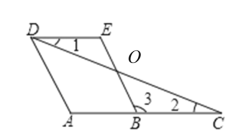
(2)如图,设BE和CD交于点O,
∵DC平分∠ADE,
∴∠ADC=∠1,
∵AD∥BE,
∴∠ADC=∠BOC=∠DOE=∠1,
∴与∠1相等的角有:∠ADC、∠BOC、∠DOE、∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的中线, DE⊥AB于E, DF⊥AC于F, 且BE=CF, 求证:(1)AD是∠BAC的平分线;(2)AB=AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠CME+∠ABF=180°,MA平分∠CMN.若∠MNA=62°,求∠A的度数.根据提示将解题过程补充完整.
解:因为∠ABM+∠ABF=180°,
又因为∠CME+∠ABF=180°(已知),
所以∠ABM=∠CME
所以AB∥CD,理由:( )
所以∠CMN+( )=180°,
理由:(__________________________)
因为∠MNA=62°,
所以∠CMN=( )
因为MA平分∠CMN,
所以∠AMC=
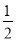 ∠CMN =( ).(角平分线的定义)
∠CMN =( ).(角平分线的定义)因为AB∥CD,
所以∠A=∠AMC=( )理由:(__________________________________)
-
科目: 来源: 题型:
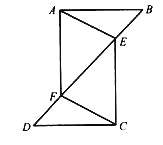
查看答案和解析>>【题目】如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两组邻边分别相等的四边形我们称它为筝形,如图,在筝形ABCD中,AB=AD,BC=DC,AC,BD相交于点O.

(1)求证:①△ABC≌△ADC;②OB=OD,AC⊥BD;
(2)如果AC=6,BD=4,求筝形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B
 C
C D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
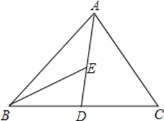
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
(1)若∠ABE=20°,∠BAD=45°,求∠BED的度数;
(2)画出△BED中BD边上的高;
(3)若△ABC的面积为80,BD=8,则点E到BC边的距离为多少?
相关试题

