搜索
【题目】如图，在菱形ABCD中，边长为10，∠A=60°．顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去…．则四边形A2B2C2D2的周长是；四边形A2013B2013C2013D2013的周长是 ． 
参考答案：
【答案】20；
【解析】解：∵菱形ABCD中，边长为10，∠A=60°，顺次连结菱形ABCD各边中点， ∴△AA1D1是等边三角形，四边形A2B2C2D2是菱形，
∴A1D1=5，C1D1= 
AC=5 
，A2B2=C2D2=C2B2=A2D2=5，
∴四边形A2B2C2D2的周长是：5×4=20，
同理可得出：A3D3=5× ，C3D3= C1D1= ×5 ，
A5D5=5×（ ）2 ， C5D5= C3D3=（ ）2×5 ，
…
∴四边形A2013B2013C2013D2013的周长是： 
= ．
故答案为：20； ．
根据菱形的性质以及三角形中位线的性质以及勾股定理求出四边形各边长得出规律求出即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】学校计划从商店购买同一品牌的钢笔和文具盒，已知购买一个文具盒比购买一个钢笔多用20元，若用400元购买文具盒和用160元购买钢笔，则购买文具盒的个数是购买钢笔个数的一半．
（1）分别求出该品牌文具盒、钢笔的定价；
（2）经商谈，商店给予学校购买一个该品牌文具盒赠送一个该品牌钢笔的优惠，如果学校需要钢笔的个数是文具盒个数的2倍还多8个，且学校购买文具盒和钢笔的总费用不超过670元，那么该学校最多可购买多少个该品牌文具盒？ -
科目： 来源： 题型：
查看答案和解析>>【题目】在⊙O中，弦AB、CD相交于点E，连接AC、BC，AC=BC，AB=CD．
（1）如图1，求证：BE平分∠CBD；
（2）如图2，F为BC上一点，连接AF交CD于点G，当∠FAB=
∠ACB时，求证：AC=BD+2CF；
（3）如图3，在（2）的条件下，若S△ACF=S△CBD ， ⊙O的半径为3
，求线段GD的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，抛物线y=ax2﹣5ax+4a与x轴交于A、B（A点在B点的左侧）与y轴交于点C．
（1）如图1，连接AC、BC，若△ABC的面积为3时，求抛物线的解析式；
（2）如图2，点P为第四象限抛物线上一点，连接PC，若∠BCP=2∠ABC时，求点P的横坐标；
（3）如图3，在（2）的条件下，点F在AP上，过点P作PH⊥x轴于H点，点K在PH的延长线上，AK=KF，∠KAH=∠FKH，PF=﹣4
a，连接KB并延长交抛物线于点Q，求PQ的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
在数学课上，老师提出如下问题：
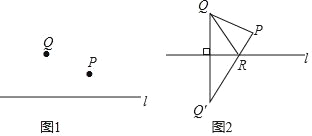
如图1，P，Q是直线l同侧两点，请你在直线l上确定一个点R，使△PQR的周长最小．
小阳的解决方法如下：
如图2，
（1）作点Q关于直线l的对称点Q；
（2）连接PQ′交直线l于点R；
（3）连接RQ，PQ．
所以点R就是使△PQR周长最小的点．
老师说：“小阳的作法正确．”
请回答：小阳的作图依据是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将一块三角板和半圆形量角器按图中方式叠放，三角板一边与量角器的零刻度线所在直线重合，重叠部分的量角器弧（
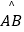）对应的圆心角（∠AOB）为120°，OC的长为2cm，则三角板和量角器重叠部分的面积为 ．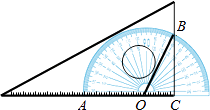 
-
科目： 来源： 题型：
查看答案和解析>>【题目】小芳同学有两根长度为4cm、10cm的木棒，她想钉一个三角形相框，桌上有五根木棒供她选择（如图所示），从中任选一根，能钉成三角形相框的概率是 ．
相关试题
