【题目】在⊙O中,弦AB、CD相交于点E,连接AC、BC,AC=BC,AB=CD. 
(1)如图1,求证:BE平分∠CBD;
(2)如图2,F为BC上一点,连接AF交CD于点G,当∠FAB= ![]() ∠ACB时,求证:AC=BD+2CF;
∠ACB时,求证:AC=BD+2CF;
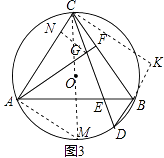
(3)如图3,在(2)的条件下,若S△ACF=S△CBD , ⊙O的半径为3 ![]() ,求线段GD的长.
,求线段GD的长.
参考答案:
【答案】
(1)证明:∵AB=CD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵AC=BC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴∠ABC=∠ABD,
∴BE平分∠CBD
(2)证明:
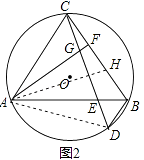
如图2,在线段BF上取点H,使FH=FC,连接AH,AD,
∵AC=BC,∴∠CAB=∠CBA,
∵在△ABC中,∠CAB+∠CBA+∠ACB=180°,
∴∠CBA+ ![]() ∠ACB=90°,
∠ACB=90°,
∵∠FAB= ![]() ∠ACB,
∠ACB,
∴∠FAB+∠CBA=90°,
∴∠AFB=90°,
∴AF⊥CH,
∵CF=FH,
∴AC=AH,
∴∠ACB=∠AHC,
∵A、C、B、D四点在⊙O上,
∴∠ACB+∠ADB=180°,
∵∠AHC+∠AHB=180°,
∴∠AHB=∠ADB,
∵∠ABC=∠ABD,AB=AB,
在△AHB与△ADB中,
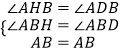 ,
,
∴△AHB≌△ADB,
∴BD=BH,
∵AC=BC=CF+FH+HB,
∴AC=BD+2CF
(3)解:如图3,过点C作CK⊥BD于点K,作直径CM,连接AM,
∵∠CBA=∠CAB=∠ABD,
∴AC∥BD,
∴∠CBK=∠ACB,∠CKB=∠AFC,AC=BC,
在△AFC与△CKB中, 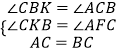 ,
,
∴△AFC≌△CKB,
∴S△AFC=S△CKB=S△CBD,
∴BD=BK=CF,
∵AC=BD+2CF,
∴AC=3CF=3BD,
设BD=CF=k,则AC=BC=3k,BF=2k,
在Rt△ACF中,由勾股定理得:AF=2 ![]() k,
k,
在Rt△AFB中,tan∠FBA= ![]() ,
,
∵CM为⊙O的直径,
∴∠CAM=90°,
∵∠CMA=∠CBA,
在Rt△ACM中,AC=3k,tan∠CMA= ![]() ,CM=6
,CM=6 ![]() ,
,
∴AM= ![]() k,
k,
由勾股定理得:(3k)2+( ![]() )2=(6
)2=(6 ![]() )2,
)2,
∴k=4,
∴AC=12,CF=4,AF=8 ![]() ,
,
在Rt△ACF中,tan∠CAF= ![]() ,tan∠ACD=
,tan∠ACD= ![]() ,AC=12,
,AC=12,
∴CG= ![]() ,
,
在Rt△AFB中,AF=8 ![]() ,FB=8,
,FB=8,
由勾股定理得:AB=CD=8 ![]() ,
,
∴DG= ![]() .
.
【解析】(1)由AB=CD,得到 ![]() =
= ![]() ,由AC=BC,得到
,由AC=BC,得到 ![]() =
= ![]() ,于是得到
,于是得到 ![]() =
= ![]() ,根据圆周角定理即可证得结论.(2)根据全等三角形的性质得到∠CAB=∠CBA,根据三角形的内角和得到∠CBA+
,根据圆周角定理即可证得结论.(2)根据全等三角形的性质得到∠CAB=∠CBA,根据三角形的内角和得到∠CBA+ ![]() ∠ACB=90°推出AF⊥CH,得到∠ACB=∠AHC,根据圆内接四边形的性质得到∠ACB+∠ADB=180°,等量代换得到∠AHB=∠ADB,根据全等三角形的性质得到BD=BH,即可得到结论;(3)根据已知条件得到AC∥BD,根据平行线的性质得到∠CBK=∠ACB,∠CKB=∠AFC,推出△AFC≌△CKB,于是得到S△AFC=S△CKB=S△CBD , 等量代换得到AC=3CF=3BD,设BD=CF=k,则AC=BC=3k,BF=2k,根据勾股定理得到AF=2
∠ACB=90°推出AF⊥CH,得到∠ACB=∠AHC,根据圆内接四边形的性质得到∠ACB+∠ADB=180°,等量代换得到∠AHB=∠ADB,根据全等三角形的性质得到BD=BH,即可得到结论;(3)根据已知条件得到AC∥BD,根据平行线的性质得到∠CBK=∠ACB,∠CKB=∠AFC,推出△AFC≌△CKB,于是得到S△AFC=S△CKB=S△CBD , 等量代换得到AC=3CF=3BD,设BD=CF=k,则AC=BC=3k,BF=2k,根据勾股定理得到AF=2 ![]() k,由圆周角定理得到∠CAM=90°,解直角三角形得到AM=
k,由圆周角定理得到∠CAM=90°,解直角三角形得到AM= ![]() k,根据勾股定理列方程得到AC=12,CF=4,AF=8
k,根据勾股定理列方程得到AC=12,CF=4,AF=8 ![]() ,解直角三角形即可得到结论.
,解直角三角形即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y1=﹣x+4的图象与函数y2=
 (x>0)的图象交于A(a,1)、B(1,b)两点.
(x>0)的图象交于A(a,1)、B(1,b)两点. 
(1)求函数y2的表达式;
(2)观察图象,比较当x>0时,y1与y2的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=BC,在△ABC外侧作直线CP,点A关于直线CP的对称点为D,连接AD,BD,其中BD交直线CP于点E.
(1)如图1,∠ACP=15°.
①依题意补全图形;
②求∠CBD的度数;
(2)如图2,若45°<∠ACP<90°,直接用等式表示线段AC,DE,BE之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划从商店购买同一品牌的钢笔和文具盒,已知购买一个文具盒比购买一个钢笔多用20元,若用400元购买文具盒和用160元购买钢笔,则购买文具盒的个数是购买钢笔个数的一半.
(1)分别求出该品牌文具盒、钢笔的定价;
(2)经商谈,商店给予学校购买一个该品牌文具盒赠送一个该品牌钢笔的优惠,如果学校需要钢笔的个数是文具盒个数的2倍还多8个,且学校购买文具盒和钢笔的总费用不超过670元,那么该学校最多可购买多少个该品牌文具盒? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.

(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是;四边形A2013B2013C2013D2013的周长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出如下问题:
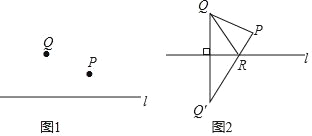
如图1,P,Q是直线l同侧两点,请你在直线l上确定一个点R,使△PQR的周长最小.
小阳的解决方法如下:
如图2,
(1)作点Q关于直线l的对称点Q;
(2)连接PQ′交直线l于点R;
(3)连接RQ,PQ.
所以点R就是使△PQR周长最小的点.
老师说:“小阳的作法正确.”
请回答:小阳的作图依据是_____.
相关试题

