【题目】在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
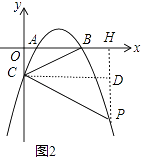
(2)如图2,点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;
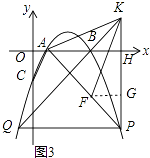
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 ![]() a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长.
参考答案:
【答案】
(1)
解:当y=0时,ax2﹣5ax+4a=0,解得x1=1,x2=4,则A(1,0),B(4,0),
∴AB=3,
∵△ABC的面积为3,
∴ ![]() 4OC=3,解得OC=2,则C(0,﹣2),
4OC=3,解得OC=2,则C(0,﹣2),
把C(0,﹣2)代入y=ax2﹣5ax+4a得4a=﹣2,解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x﹣2
x﹣2
(2)
解:过点P作PH⊥x轴于H,作CD⊥PH于点H,如图2,设P(x,ax2﹣5ax+4a),则PD=4a﹣(ax2﹣5ax+4a)=﹣ax2+5ax,
∵AB∥CD,
∴∠ABC=∠BCD,
∵∠BCP=2∠ABC,
∴∠PCD=∠ABC,
∴Rt△PCD∽Rt△CBO,
∴PD:OC=CD:OB,
即(﹣ax2+5ax):(﹣4a)=x:4,解得x1=0,x2=6,
∴点P的横坐标为6
(3)
解:过点F作FG⊥PK于点G,如图3,
∵AK=FK,
∴∠KAF=∠KFA,
而∠KAF=∠KAH+∠PAH,∠KFA=∠PKF+∠KPF,
∵∠KAH=∠FKP,
∴∠HAP=∠KPA,
∴HA=HP,
∴△AHP为等腰直角三角形,
∵P(6,10a),
∴﹣10a=6﹣1,解得a=﹣ ![]() ,
,
在Rt△PFG中,∵PF=﹣4 ![]() a=2
a=2 ![]() ,∠FPG=45°,
,∠FPG=45°,
∴FG=PG= ![]() PF=2,
PF=2,
在△AKH和△KFG中
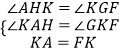 ,
,
∴△AKH≌△KFG,
∴KH=FG=2,
∴K(6,2),
设直线KB的解析式为y=mx+n,
把K(6,2),B(4,0)代入得 ![]() ,
,
解得 ![]() ,
,
∴直线KB的解析式为y=x﹣4,
当a=﹣ ![]() 时,抛物线的解析式为y=﹣
时,抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x﹣2,
x﹣2,
解方程组 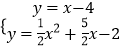 ,
,
解得 ![]() 或
或 ![]() ,
,
∴Q(﹣1,﹣5),
而P(6,﹣5),
∴PQ∥x 轴,
∴QP=7.
【解析】(1)通过解方程ax2﹣5ax+4a=0可得到A(1,0),B(4,0),然后利用三角形面积公式求出OC得到C点坐标,再把C点坐标代入y=ax2﹣5ax+4a中求出a即可得到抛物线的解析式;(2)过点P作PH⊥x轴于H,作CD⊥PH于点H,如图2,设P(x,ax2﹣5ax+4a),则PD=﹣ax2+5ax,通过证明Rt△PCD∽Rt△CBO,利用相似比可得到(﹣ax2+5ax):(﹣4a)=x:4,然后解方程求出x即可得到点P的横坐标;(3)过点F作FG⊥PK于点G,如图3,先证明∠HAP=∠KPA得到HA=HP,由于P(6,10a),则可得到﹣10a=6﹣1,解得a=﹣ ![]() ,再判断Rt△PFG单位等腰直角三角形得到FG=PG=
,再判断Rt△PFG单位等腰直角三角形得到FG=PG= ![]() PF=2,接着证明△AKH≌△KFG,得到KH=FG=2,则K(6,2),然后利用待定系数法求出直线KB的解析式为y=x﹣4,再通过解方程组
PF=2,接着证明△AKH≌△KFG,得到KH=FG=2,则K(6,2),然后利用待定系数法求出直线KB的解析式为y=x﹣4,再通过解方程组 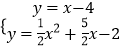 得到Q(﹣1,﹣5),利用P、Q点的坐标可判断PQ∥x 轴,于是可得到QP=7.
得到Q(﹣1,﹣5),利用P、Q点的坐标可判断PQ∥x 轴,于是可得到QP=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=BC,在△ABC外侧作直线CP,点A关于直线CP的对称点为D,连接AD,BD,其中BD交直线CP于点E.
(1)如图1,∠ACP=15°.
①依题意补全图形;
②求∠CBD的度数;
(2)如图2,若45°<∠ACP<90°,直接用等式表示线段AC,DE,BE之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划从商店购买同一品牌的钢笔和文具盒,已知购买一个文具盒比购买一个钢笔多用20元,若用400元购买文具盒和用160元购买钢笔,则购买文具盒的个数是购买钢笔个数的一半.
(1)分别求出该品牌文具盒、钢笔的定价;
(2)经商谈,商店给予学校购买一个该品牌文具盒赠送一个该品牌钢笔的优惠,如果学校需要钢笔的个数是文具盒个数的2倍还多8个,且学校购买文具盒和钢笔的总费用不超过670元,那么该学校最多可购买多少个该品牌文具盒? -
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,弦AB、CD相交于点E,连接AC、BC,AC=BC,AB=CD.

(1)如图1,求证:BE平分∠CBD;
(2)如图2,F为BC上一点,连接AF交CD于点G,当∠FAB= ∠ACB时,求证:AC=BD+2CF;
∠ACB时,求证:AC=BD+2CF;
(3)如图3,在(2)的条件下,若S△ACF=S△CBD , ⊙O的半径为3 ,求线段GD的长.
,求线段GD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是;四边形A2013B2013C2013D2013的周长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出如下问题:
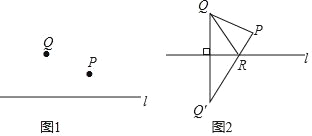
如图1,P,Q是直线l同侧两点,请你在直线l上确定一个点R,使△PQR的周长最小.
小阳的解决方法如下:
如图2,
(1)作点Q关于直线l的对称点Q;
(2)连接PQ′交直线l于点R;
(3)连接RQ,PQ.
所以点R就是使△PQR周长最小的点.
老师说:“小阳的作法正确.”
请回答:小阳的作图依据是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧(
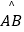 )对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 .
)对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 . 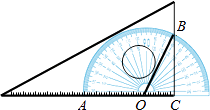
相关试题

