【题目】阅读下面材料:
在数学课上,老师提出如下问题:
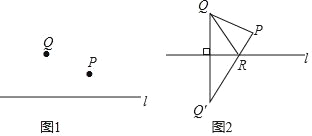
如图1,P,Q是直线l同侧两点,请你在直线l上确定一个点R,使△PQR的周长最小.
小阳的解决方法如下:
如图2,
(1)作点Q关于直线l的对称点Q;
(2)连接PQ′交直线l于点R;
(3)连接RQ,PQ.
所以点R就是使△PQR周长最小的点.
老师说:“小阳的作法正确.”
请回答:小阳的作图依据是_____.
参考答案:
【答案】如果两个图形关于某直线对称,那么对称轴是对称点连线的垂直平分线:线段垂直平分线上的点到线段两个端点的距离相等:两点之间线段最短
【解析】
根据轴对称的性质解答即可.
根据题意,得:小阳的作图依据是:如果两个图形关于某直线对称,那么对称轴是对称点连线的垂直平分线;线段垂直平分线上的点到线段两个端点的距离相等;两点之间线段最短.
故答案为:如果两个图形关于某直线对称,那么对称轴是对称点连线的垂直平分线;线段垂直平分线上的点到线段两个端点的距离相等;两点之间线段最短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,弦AB、CD相交于点E,连接AC、BC,AC=BC,AB=CD.

(1)如图1,求证:BE平分∠CBD;
(2)如图2,F为BC上一点,连接AF交CD于点G,当∠FAB= ∠ACB时,求证:AC=BD+2CF;
∠ACB时,求证:AC=BD+2CF;
(3)如图3,在(2)的条件下,若S△ACF=S△CBD , ⊙O的半径为3 ,求线段GD的长.
,求线段GD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.

(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是;四边形A2013B2013C2013D2013的周长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧(
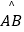 )对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 .
)对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 . 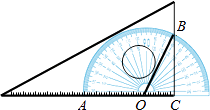
-
科目: 来源: 题型:
查看答案和解析>>【题目】小芳同学有两根长度为4cm、10cm的木棒,她想钉一个三角形相框,桌上有五根木棒供她选择(如图所示),从中任选一根,能钉成三角形相框的概率是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论正确的是( )
A.x2﹣2是二次二项式
B.单项式﹣x2的系数是1
C.使式子 有意义的x的取值范围是x>﹣2
有意义的x的取值范围是x>﹣2
D.若分式 的值等于0,则a=±1
的值等于0,则a=±1
相关试题

