【题目】如图,在平面直角坐标系中,点A(1, ![]() ),点B(2,0),P为线段OB上一点,过点P作PQ∥OA,交AB于点Q,连接AP,则△APQ面积最大值为( )
),点B(2,0),P为线段OB上一点,过点P作PQ∥OA,交AB于点Q,连接AP,则△APQ面积最大值为( ) 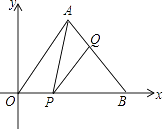
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解:如图,作AF⊥OB于F,QE⊥OB于E.设OP=x, 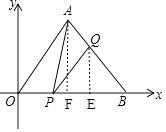 ,
,
∵点A(1, ![]() ),点B(2,0),
),点B(2,0),
∴点F是OB的中点,
∴OF=2÷2=1,AF= ![]() ,
,
∵OF=FB,AF⊥OB,
∴AO=AB,
∴OA=AB= ![]() =2,
=2,
∵OA=AB=OB=2,
∴△AOB是等边三角形,
∴∠BOA=∠BAO=∠ABO=60°,
∵PQ∥OA,
∴∠QPB=∠AOB=60°,
∴△BPQ是等边三角形,
∴BP=BQ=PQ=2﹣x,
∴S△BPQ= ![]() (2﹣x)2 ,
(2﹣x)2 ,
∴S△APQ=S△AOB﹣S△AOP﹣S△BPQ
= ![]() ×22﹣
×22﹣ ![]() x
x ![]() ﹣
﹣ ![]() (2﹣x)2
(2﹣x)2
= ![]() ﹣
﹣ ![]() x﹣
x﹣ ![]() ×(4﹣2x+x2)
×(4﹣2x+x2)
=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
≤ ![]()
∴当x=1时,△APQ面积最大值为 ![]() .
.
故选:B.
【考点精析】关于本题考查的二次函数的最值和相似三角形的判定与性质,需要了解如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三条角平分线相交于点I,过点I作DI⊥IC,交AC于点D.
(1)如图①,求证:∠AIB=∠ADI;
(2)如图②,延长BI,交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系,并说明理由;
②若∠BAC=70°,求∠F的度数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】服装店10月份以每套500元的进价购进一批羽绒服,当月以标价销售,销售额14000元,进入11月份搞促销活动,每件降价50元,这样销售额比10月份增加了5500元,售出的件数是10月份的1.5倍.
(1)求每件羽绒服的标价是多少元;
(2)进入12月份,该服装店决定把剩余的羽绒服按10月份标价的八折销售,结果全部卖掉,而且这批羽绒服总获利不少于12700元,问这批羽绒服至少购进多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC=90°,AB=DB,EB=CB,M,N分别是AE,CD的中点.
(1)求证:△ABM≌△DBN;
(2)试探索BM和BN的关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C,D在⊙O上,
 =2
=2  ,
,  =3
=3  ,延长BC,AD交于点P,若∠CBD=18°,则∠P的大小为 .
,延长BC,AD交于点P,若∠CBD=18°,则∠P的大小为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点E为矩形ABCD外一点,连接AE,DE,且AE=DE,连接EB,EC分别与AD相交于点F,G.
(1)如图1,求证:∠ABE=∠DCE;
(2)如图2,若△BCE是等边三角形,且AE=AB,在不添加任何辅助线的情况下,请直接写出图2中四对全等的钝角三角形.
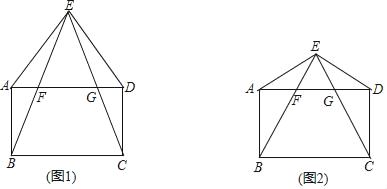
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)
 =2﹣
=2﹣
(2)
 ﹣
﹣ =﹣1
=﹣1
相关试题

