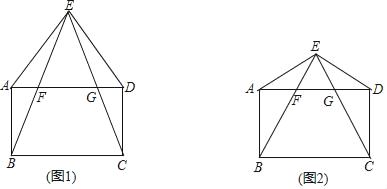
【题目】已知:点E为矩形ABCD外一点,连接AE,DE,且AE=DE,连接EB,EC分别与AD相交于点F,G.
(1)如图1,求证:∠ABE=∠DCE;
(2)如图2,若△BCE是等边三角形,且AE=AB,在不添加任何辅助线的情况下,请直接写出图2中四对全等的钝角三角形.
参考答案:
【答案】(1)证明见解析(2)△ABE≌△DCE,△ABE≌△EAD,△EAD≌△EDC,△AFE≌△DGE
【解析】
(1)先由四边形ABCD是矩形,得出AB=DC,∠BAD=∠CDA=90°.由EA=ED,得出∠EAD=∠EDA,根据等式的性质得到∠EAB=∠EDC.然后利用SAS即可证明△EAB≌△EDC;
(2)题意可知,△ABE,△DCE,△EAD都是顶角为120°的等腰三角形,且AB=AE=ED=CD,△AFE,△DGE都是顶角为120°的等腰三角形且AE=ED,由此即可判断.
(1)∵四边形ABCD是矩形,
∴AB=DC,∠BAD=∠CDA=90°,
∵EA=ED,
∴∠EAD=∠EDA,
∴∠EAB=∠EDC,
在△EAB与△EDC中,
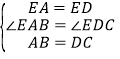 ,
,
∴△EAB≌△EDC(SAS),
∴∠ABE=∠DCE;
(2)由题意可知,△ABE,△DCE,△EAD都是顶角为120°的等腰三角形,且AB=AE=ED=CD,
∴△ABE≌△DCE,△ABE≌△EAD,△EAD≌△EDC,
∵△AFE,△DGE都是顶角为120°的等腰三角形且AE=ED,
∴△AFE≌△DGE.
∴四对全等的钝角三角形有:△ABE≌△DCE,△ABE≌△EAD,△EAD≌△EDC,△AFE≌△DGE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC=90°,AB=DB,EB=CB,M,N分别是AE,CD的中点.
(1)求证:△ABM≌△DBN;
(2)试探索BM和BN的关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(1,
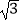 ),点B(2,0),P为线段OB上一点,过点P作PQ∥OA,交AB于点Q,连接AP,则△APQ面积最大值为( )
),点B(2,0),P为线段OB上一点,过点P作PQ∥OA,交AB于点Q,连接AP,则△APQ面积最大值为( ) 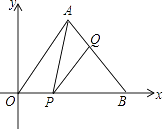
A.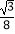
B.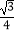
C.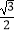
D.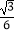
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C,D在⊙O上,
 =2
=2  ,
,  =3
=3  ,延长BC,AD交于点P,若∠CBD=18°,则∠P的大小为 .
,延长BC,AD交于点P,若∠CBD=18°,则∠P的大小为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)
 =2﹣
=2﹣
(2)
 ﹣
﹣ =﹣1
=﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】试验与探究:我们知道分数
 写为小数即
写为小数即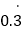 ,反之,无限循环小数
,反之,无限循环小数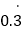 写成分数即
写成分数即 .一般地,任何一个无限循环小数都可以写成分数形式.现在就以
.一般地,任何一个无限循环小数都可以写成分数形式.现在就以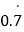 为例进行讨论:设
为例进行讨论:设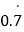 =x,由
=x,由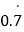 =0.7777…,可知,10x﹣x=7.77…﹣0.777…=7,即10x﹣x=7,解方程得
=0.7777…,可知,10x﹣x=7.77…﹣0.777…=7,即10x﹣x=7,解方程得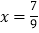 ,于是得
,于是得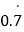 =
= .
.请仿照上述例题完成下列各题:
(1)请你把无限循环小数
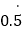 写成分数,即
写成分数,即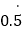 =_____.
=_____.(2)你能化无限循环小数
 为分数吗?请仿照上述例子求解之.
为分数吗?请仿照上述例子求解之. -
科目: 来源: 题型:
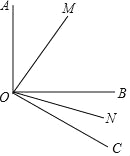
查看答案和解析>>【题目】如图,已知OM平分∠AOB,ON平分∠BOC.
(1)若∠AOB=90°,∠BOC=30°,则∠MON=_____;
(2)若∠AOB=α,∠BOC=β,其它条件不变,则∠MON=______;
(3)当OC运动到∠AOB内部时,其余条件不变,请你画出图形并猜想∠MON与∠AOB、∠BOC的数量关系式,并说明理由.
相关试题

