【题目】如图,△ABC的三条角平分线相交于点I,过点I作DI⊥IC,交AC于点D.
(1)如图①,求证:∠AIB=∠ADI;
(2)如图②,延长BI,交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系,并说明理由;
②若∠BAC=70°,求∠F的度数.


参考答案:
【答案】(1)证明见解析;(2)解:①结论:DI∥CF,②35°.
【解析】(1)只要证明∠AIB=90°+![]() ∠ACB,∠ADI=90°+
∠ACB,∠ADI=90°+![]() ∠ACB即可;
∠ACB即可;
(2)①只要证明∠IDC=∠DCF即可;
②首先求出∠ACE-∠ABC=∠BAC=70°,再证明∠F=![]() ∠ACE-
∠ACE-![]() ∠ABC=
∠ABC=![]() (∠ACE-∠ABC)即可解决问题;
(∠ACE-∠ABC)即可解决问题;
(1)证明:∵AI,BI分别平分∠BAC,∠ABC,
∴∠BAI=![]() ∠BAC,∠ABI=
∠BAC,∠ABI=![]() ∠ABC,
∠ABC,
∴∠BAI+∠ABI=![]() (∠BAC+∠ABC)=
(∠BAC+∠ABC)=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB.
∠ACB.
在△ABI中,∠AIB=180°-(∠BAI+∠ABI)=180°-(90°-![]() ∠ACB)=90°+
∠ACB)=90°+![]() ∠ACB.
∠ACB.
∵CI平分∠ACB,∴∠DCI=![]() ∠ACB.∵DI⊥IC,
∠ACB.∵DI⊥IC,
∴∠DIC=90°,∴∠ADI=∠DIC+∠DCI=90°+![]() ∠ACB.
∠ACB.
∴∠AIB=∠ADI.
(2)解:①结论:DI∥CF.
理由:∵∠IDC=90°-∠DCI=90°-![]() ∠ACB,CF平分∠ACE,
∠ACB,CF平分∠ACE,
∴∠ACF=![]() ∠ACE=
∠ACE=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB,∴∠IDC=∠ACF,∴DI∥CF.
∠ACB,∴∠IDC=∠ACF,∴DI∥CF.
②∵∠ACE=∠ABC+∠BAC,∴∠ACE-∠ABC=∠BAC=70°.
∵∠FCE=∠FBC+∠F,∴∠F=∠FCE-∠FBC.
∵∠FCE=![]() ∠ACE,∠FBC=
∠ACE,∠FBC=![]() ∠ABC,
∠ABC,
∴∠F=![]() ∠ACE-
∠ACE-![]() ∠ABC=
∠ABC=![]() (∠ACE-∠ABC)=35°.
(∠ACE-∠ABC)=35°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板按如图摆放,其中△ABC为含有45度角的三角板,直线AD是等腰直角三角形ABC的对称轴,且将△ABC分成两个等腰直角三角形,DM、DN分别与边AB、AC交于E、F两点,有下列四个结论:①BD=AD=CD②△AED≌△CFD③BE+CF=EF④S四边形AEDF=
 AB2.其中正确结论是_____(填写正确序号)
AB2.其中正确结论是_____(填写正确序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有
 、
、 两种型号的客车共20辆,它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下,共载客720人.
两种型号的客车共20辆,它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下,共载客720人.A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
(1)求
 、
、 两种型号的客车各有多少辆?
两种型号的客车各有多少辆?(2)某中学计划租用
 、
、 两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车?
两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(﹣5,2),将△ABC沿x轴向右平移得到△A1B1C1 , 使得点B1恰好落在函数y=
 上,若线段AC扫过的面积为48,则点C1的坐标为( )
上,若线段AC扫过的面积为48,则点C1的坐标为( ) 
A.(3,2)
B.(5,6)
C.(8,6)
D.(6,6) -
科目: 来源: 题型:
查看答案和解析>>【题目】服装店10月份以每套500元的进价购进一批羽绒服,当月以标价销售,销售额14000元,进入11月份搞促销活动,每件降价50元,这样销售额比10月份增加了5500元,售出的件数是10月份的1.5倍.
(1)求每件羽绒服的标价是多少元;
(2)进入12月份,该服装店决定把剩余的羽绒服按10月份标价的八折销售,结果全部卖掉,而且这批羽绒服总获利不少于12700元,问这批羽绒服至少购进多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC=90°,AB=DB,EB=CB,M,N分别是AE,CD的中点.
(1)求证:△ABM≌△DBN;
(2)试探索BM和BN的关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(1,
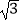 ),点B(2,0),P为线段OB上一点,过点P作PQ∥OA,交AB于点Q,连接AP,则△APQ面积最大值为( )
),点B(2,0),P为线段OB上一点,过点P作PQ∥OA,交AB于点Q,连接AP,则△APQ面积最大值为( ) 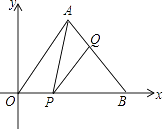
A.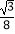
B.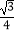
C.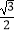
D.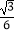
相关试题

