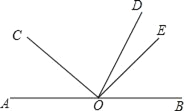
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.
(1)求证:OD=OC;
(2)若∠AOB=60°,求证:OE=4EF.

参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)利用角平分线定理得到ED=EC,再由斜边为公共边,利用HL得到直角三角形ODE与直角三角形OCE全等,利用全等三角形的对应边相等即可得证;
(2)由OE为角平分线,且∠AOB=60°,得到∠DOE=∠EDF=30°,在直角三角形ODE中,利用30度角所对的直角边等于斜边的一半得到OE=2DE,在直角三角形DEF中,利用30度角所对的直角边等于斜边的一半得到DE=2EF,等量代换即可得证.
证明:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴ED=EC,
在Rt△ODE和Rt△OCE中,
![]() ,
,
∴Rt△ODE≌Rt△OCE(HL),
∴OD=OC;
(2)∵∠AOB=60°,OE平分∠AOB,
∴∠DOE=∠COE=30°,
∴∠DEO=60°,∠EDF=30°,
∵在Rt△ODE中,∠DOE=30°,
∴OE=2DE,
∵在Rt△DEF中,∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在
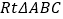 中,
中, 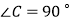 ,
, 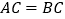 ,
, 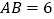 ,点
,点 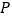 是
是 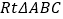 的重心,则点
的重心,则点 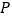 到
到 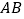 所在直线的距离等于( )
所在直线的距离等于( )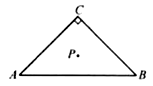
A.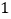
B.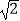
C.
D.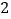
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知∠1=115°,∠2=50°,∠3=65°,又∠NEG=∠GEB,试判断AB∥CD,EG∥FH是否成立,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在每个小正方形的边长为
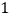 的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距
的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距 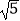 的另一个格点的运动称为一次跳马变换.例如,在
的另一个格点的运动称为一次跳马变换.例如,在  的正方形网格图形中(如图1),从点
的正方形网格图形中(如图1),从点 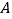 经过一次跳马变换可以到达点
经过一次跳马变换可以到达点 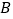 ,
, 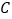 ,
,  ,
, 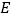 等处.现有
等处.现有  的正方形网格图形(如图2),则从该正方形的顶点
的正方形网格图形(如图2),则从该正方形的顶点 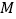 经过跳马变换到达与其相对的顶点
经过跳马变换到达与其相对的顶点  ,最少需要跳马变换的次数是( )
,最少需要跳马变换的次数是( )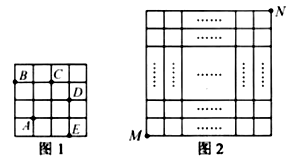
A.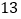
B.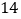
C.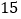
D.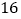
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
(1)若∠AOC=48°,求∠DOE的度数.
(2)若∠AOC=α,则∠DOE= (用含α的代数式表示).
相关试题

