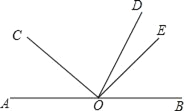
【题目】如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
(1)若∠AOC=48°,求∠DOE的度数.
(2)若∠AOC=α,则∠DOE= (用含α的代数式表示).
参考答案:
【答案】(1) ∠DOE=24°;(2)![]() α.
α.
【解析】
(1)先由邻补角定义求出∠BOC=180°-∠AOC=132°,再根据角平分线定义得到∠COD=![]() ∠BOC=66°,那么∠DOE=∠COE-∠COD=24°;
∠BOC=66°,那么∠DOE=∠COE-∠COD=24°;
(2)先由邻补角定义求出∠BOC=180°-∠AOC=180°-α,再根据角平分线定义得到∠COD=![]() ∠BOC,于是得到结论.
∠BOC,于是得到结论.
解:(1)∵O是直线AB上一点,
∴∠AOC+∠BOC=180°,
∵∠AOC=48°,
∴∠BOC=132°,
∵OD平分∠BOC,
∴∠COD=![]() ∠BOC=66°,
∠BOC=66°,
∵∠DOE=∠COE﹣∠COD,∠COE=90°,
∴∠DOE=90°﹣66°=24°;
(2)∵O是直线AB上一点,
∴∠AOC+∠BOC=180°,
∵∠AOC=α,
∴∠BOC=180°﹣α,
∵OD平分∠BOC,
∴∠COD=![]() ∠BOC=
∠BOC=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α,
α,
∵∠DOE=∠COE﹣∠COD,∠COE=90°,
∴∠DOE=90°﹣(90°﹣![]() α)=
α)=![]() α.
α.
故答案为:![]() α.
α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a﹣1)x+m的图象可能是( )

A.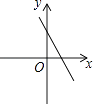
B.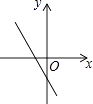
C.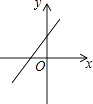
D.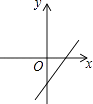
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是⊙O上一点,⊙O的半径为
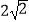 ,D、E分别是弦AC、BC上一动点,且OD=OE=
,D、E分别是弦AC、BC上一动点,且OD=OE= 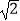 ,则AB的最大值为( )
,则AB的最大值为( ) 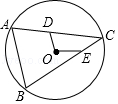
A.
B.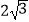
C.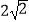
D.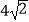
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,老师提出如下问题: 如图1,将锐角三角形纸片ABC(BC>AC)经过两次折叠,得到边AB,BC,CA上的点D,E,F.使得四边形DECF恰好为菱形.
小明的折叠方法如下:
如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D; (2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.
老师说:“小明的作法正确.”
请回答:小明这样折叠的依据是 .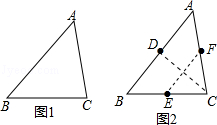
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④4a﹣2b+c>0,其中正确的个数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2sin45°﹣(
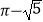 )0
)0 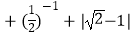 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.

相关试题

