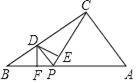
【题目】如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点P在边AB上,∠CPB的平分线交边BC于点D,DE⊥CP于点E,DF⊥AB于点F.当△PED与△BFD的面积相等时,BP的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】D
【解析】
根据勾股定理得到AB=5,根据角平分线的性质得到DE=DF,根据全等三角形的性质得到BF=PF,根据相似三角形的性质即可得到结论.
解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=5,
∵PD平分∠BPC,DF⊥PB,DE⊥PC,
∴DE=DF,
在Rt△PDF与Rt△PDE中,![]() ,
,
∴Rt△PDF≌Rt△PDE(HL),
∴S△PDF=S△PDE,
当△PED与△BFD的面积相等时,
∴S△PDF=S△BDF,
∴BF=PF,
∴BD=PD,
∴∠B=∠BPD=∠CPD,
∵∠BFD=∠ACB=90°,
∴△BDF∽△BAC,
∴![]() ,
,
∴![]() ,
,
∵∠PCD=∠BCP,
∴△BCP∽△PCD,
∴![]() ,
,
∴PC=![]() ,
,
∴CD=![]() ,
,
∴BD=![]() ,
,
∴PB=![]() .
.
故选:D.
-
科目: 来源: 题型:
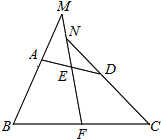
查看答案和解析>>【题目】如图,在四边形ABCD中,E、F分别是AD、BC的中点,连接FE并延长,分别交CD的延长线于点M、N,∠BME=∠CNE,求证:AB=CD.
-
科目: 来源: 题型:
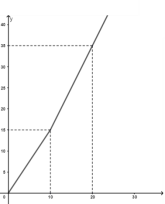
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一。为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费。即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费。设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示。
(1)求a的值;某户居民上月用水8吨,应收水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数关系式;
(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点O为△ABC的两条角平分线的交点,过点O作OD⊥BC于点D,且OD=4.若△ABC的周长是17,则△ABC的面积为( )

A. 34B. 17C. 8.5D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市的空气质量情况,从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).请你根据图中提供的信息,解答下列问题:
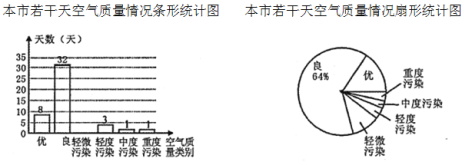
(1)通过计算补全条形统计图;
(2)求扇形统计图中表示“轻度污染”的扇形的圆心角度数;
(3)请估计我市这一年(365天)达到“优”和“良”的总天数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在反比例函数y=
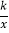 (x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
(x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.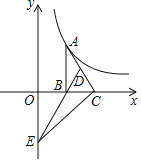
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前节能灯在城市已基本普及,为满足消费者需求,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、标价如下表:
进价(元/只)
标价(元/只)
甲型
25
40
乙型
45
60
(1)如何进货才能保证进货款恰好为46000元?
(2)由于恰逢五一,商场决定搞促销活动,乙型节能灯打八五折,请你运用所学的知识预算一下甲型节能灯要打几折才能使这批灯售完后获得9200元的利润(不考虑其它因素)?
相关试题

