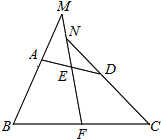
【题目】如图,在四边形ABCD中,E、F分别是AD、BC的中点,连接FE并延长,分别交CD的延长线于点M、N,∠BME=∠CNE,求证:AB=CD.
参考答案:
【答案】证明见解析
【解析】试题分析: 首先连接BD,取BD的中点G,连接EG、FG,证明GE为△ABD的中位线,得到GE=![]() AB;然后同理可证:GF=
AB;然后同理可证:GF=![]() CD,进而得到GE=GF,再结合线段间的等量代换即可解决问题.
CD,进而得到GE=GF,再结合线段间的等量代换即可解决问题.
试题解析:证明:连接BD,取BD的中点G,连接EG、FG.
∵点E、G分别为AD、BD的中点,
∴GE为△ABD的中位线,
∴GE=![]() AB.
AB.
同理可证:GF=12CD.
∵GE为△ABD的中位线,
∴GE∥MB,
∴∠GEF=∠BMF.
同理可证:∠GFE=∠CNE.
∵∠BME=∠CNE,
∴∠GEF=∠GFE,
∴GE=GF,
∴AB=CD.
-
科目: 来源: 题型:
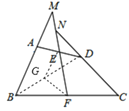
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,连结CP并延长CP交AD于Q点.给出以下结论:
①四边形AECF为平行四边形;
②∠PBA=∠APQ;
③△FPC为等腰三角形;
④△APB≌△EPC.
其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.如图,设动点P所经过的路程为x,△APD的面积为y.(当点P与点A或D重合时,y=0)
(1)写出y与x之间的函数解析式;
(2)画出此函数的图象.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=
 S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
-
科目: 来源: 题型:
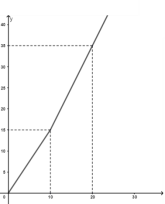
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一。为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费。即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费。设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示。
(1)求a的值;某户居民上月用水8吨,应收水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数关系式;
(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点O为△ABC的两条角平分线的交点,过点O作OD⊥BC于点D,且OD=4.若△ABC的周长是17,则△ABC的面积为( )

A. 34B. 17C. 8.5D. 4
-
科目: 来源: 题型:
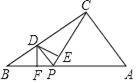
查看答案和解析>>【题目】如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点P在边AB上,∠CPB的平分线交边BC于点D,DE⊥CP于点E,DF⊥AB于点F.当△PED与△BFD的面积相等时,BP的值为( )
A.
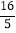 B.
B.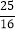 C.
C. D.
D.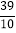
相关试题

