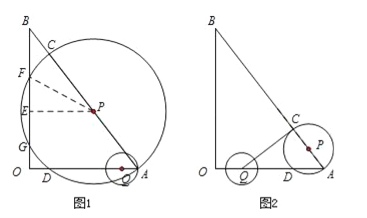
【题目】如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
(3)若⊙P与线段QC只有一个公共点,求t的取值范围.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)0<t≤
;(3)0<t≤![]() 或
或![]() <t≤5.
<t≤5.
【解析】(1)∵OA=6,OB=8,∴由勾股定理可求得:AB=10,由题意知:OQ=AP=t,∴AC=2t,∵AC是⊙P的直径,∴∠CDA=90°,∴CD∥OB,∴△ACD∽△ABO,∴![]() ,∴AD=
,∴AD=![]() ,当Q与D重合时,AD+OQ=OA,∴
,当Q与D重合时,AD+OQ=OA,∴![]() ,∴t=
,∴t=![]() ;
;
(2)当⊙Q经过A点时,如图1,OQ=OA﹣QA=4,∴t=![]() =4s,∴PA=4,∴BP=AB﹣PA=6,过点P作PE⊥OB于点E,⊙P与OB相交于点F、G,连接PF,∴PE∥OA,∴△PEB∽△AOB,∴
=4s,∴PA=4,∴BP=AB﹣PA=6,过点P作PE⊥OB于点E,⊙P与OB相交于点F、G,连接PF,∴PE∥OA,∴△PEB∽△AOB,∴![]() ,∴PE=
,∴PE=![]() ,∴由勾股定理可求得:EF=
,∴由勾股定理可求得:EF=![]() ,由垂径定理可求知:FG=2EF=
,由垂径定理可求知:FG=2EF=![]() ;
;
(3)当QC与⊙P相切时,如图2,此时∠QCA=90°,∵OQ=AP=t,∴AQ=6﹣t,AC=2t,∵∠A=∠A,∠QCA=∠ABO,∴△AQC∽△ABO,∴![]() ,∴
,∴![]() ,∴t=
,∴t=![]() ,∴当0<t≤
,∴当0<t≤![]() 时,⊙P与QC只有一个交点;
时,⊙P与QC只有一个交点;
当QC⊥OA时,此时Q与D重合,由(1)可知:t=![]() ,∴当
,∴当![]() <t≤5时,⊙P与QC只有一个交点,综上所述,当,⊙P与QC只有一个交点,t的取值范围为:0<t≤
<t≤5时,⊙P与QC只有一个交点,综上所述,当,⊙P与QC只有一个交点,t的取值范围为:0<t≤![]() 或
或![]() <t≤5.
<t≤5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】应用方程组解决实际问题的步骤:理解问题;____________;____________;____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个相似多边形面积比为4:9,则它们的周长比是________.
-
科目: 来源: 题型:
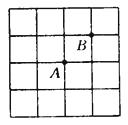
查看答案和解析>>【题目】已知在正方形网格中,每个小方格都是边长为1的正方形,A和B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形的面积为1个平方单位,则C点的个数为( ).
A.3个
B.4个
C.5个
D.6个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
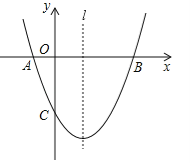
 (a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业成立3年来,累计向国家上缴利税728万元,其中第一年上缴200万元,后两年的年平均增长率相同,求第3年上缴利税多少万元.。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.零是正数不是负数
B.零既不是正数也不是负数
C.零既是正数也是负数
D.不是正数的数一定是负数,不是负数的数一定是正数
相关试题

