【题目】如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于点Q,PQ=3,PE=1.
(1)求证:∠ABE=∠CAD;
(2)求BP和AD的长.

参考答案:
【答案】(1)见解析;(2)7
【解析】
(1)根据SAS证明△ABE与△CAD全等即可得出结论;
(2)根据含30°的直角三角形的性质解答即可.
解:(1)证明:∵△ABC为等边三角形
∴AB=CA,∠BAE=∠C=60°
在△ABE和△CAD中
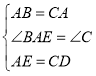
∴△ABE≌△CAD(SAS)
∴∠ABE=∠CAD
(2)在△ABP中,∠BPQ=∠ABP+∠BAP
∵∠ABP=∠CAD
∴∠BPQ=∠ABP+∠BAP=∠CAD+∠BAP=∠BAC=60°
∵BQ⊥AD,PQ=3,PE=1.
∴在Rt△BPQ中,∠BPQ=60°,则∠PBQ=30°.
∴BP=2PQ=6
∴BE=BP+PE=7.
由(1)△ABE≌△CAD,
∴AD=BE=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
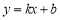 与
与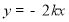 (k≠0)的图象相交于点P(1,-6).
(k≠0)的图象相交于点P(1,-6).(1)求一次函数
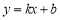 的解析式;
的解析式;(2)若点Q(m,n)在函数
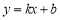 的图象上,求2n-6m+9的值.
的图象上,求2n-6m+9的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象如图所示,则在“①
的图象如图所示,则在“① ,②
,② ,③
,③ ,④
,④ ”中正确的判断是( )
”中正确的判断是( )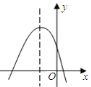
A. ①②③④ B. ④ C. ①②③ D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进
 、
、 两种新型节能台灯共
两种新型节能台灯共 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:
(
 )若商场预计进货款为
)若商场预计进货款为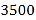 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?(
 )若商场规定
)若商场规定 型台灯的进货数量不超过
型台灯的进货数量不超过 型台灯数量的
型台灯数量的 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
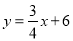 与x轴、y轴分别相交于点F,E,点A的坐标为(-6,0),P(x,y)是直线
与x轴、y轴分别相交于点F,E,点A的坐标为(-6,0),P(x,y)是直线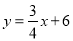 上的一个动点.
上的一个动点.(1)试写出点P在运动过程中,△OAP的面积S与x的函数关系式;
(2)当点P运动到什么位置,△OAP的面积为
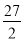 ,求出此时点P的坐标.
,求出此时点P的坐标.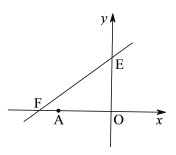
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以
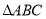 的边
的边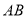 ,
, 所在直线为对称轴作
所在直线为对称轴作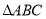 的对称图形
的对称图形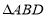 和
和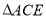 ,
, ,线段
,线段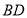 与
与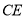 相交于点
相交于点 ,连接
,连接 、
、 、
、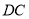 、
、 .有如下结论:①
.有如下结论:①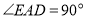 ;②
;② ;③
;③ 平分
平分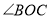 ;其中正确的结论个数是( )
;其中正确的结论个数是( )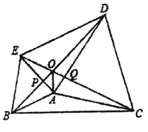
A.0个B.3个C.2个D.1个
相关试题

