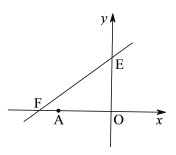
【题目】如图,直线![]() 与x轴、y轴分别相交于点F,E,点A的坐标为(-6,0),P(x,y)是直线
与x轴、y轴分别相交于点F,E,点A的坐标为(-6,0),P(x,y)是直线![]() 上的一个动点.
上的一个动点.
(1)试写出点P在运动过程中,△OAP的面积S与x的函数关系式;
(2)当点P运动到什么位置,△OAP的面积为![]() ,求出此时点P的坐标.
,求出此时点P的坐标.
参考答案:
【答案】(1)S=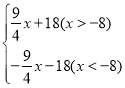 ;(2)P(-2,
;(2)P(-2,![]() )或(-14,
)或(-14,![]() )
)
【解析】
(1)设点P(x,y),将△OAP的面积表示出来,并分点P在第一、二象限和点P在第三象限两种情况进行讨论即可;
(2)分别把S=![]() 代入(1)中两种情况下的函数关系式,求出点P的横坐标,再分别代入
代入(1)中两种情况下的函数关系式,求出点P的横坐标,再分别代入![]() 中可求出点P纵坐标.
中可求出点P纵坐标.
解:(1)∵P(x,y),
∴P到x轴的距离为![]() ,
,
∵点A的坐标为(-6,0),
∴OA=6
∴S△OAP=![]() OA
OA![]()
令![]() =0,
=0,
解得x=-8,
∴F(-8,0),
①当点P在第一、二象限时,S=![]() ×6y,
×6y,![]() ,
,
∴S=![]() x+18(x>-8),
x+18(x>-8),
②当点P在第三象限时,S=![]() ×6(-y)
×6(-y)
∴S=-![]() x-18(x<-8),
x-18(x<-8),
∴点P在运动过程中,△OAP的面积S与x的函数关系式为:S=![]() x+18(x>-8)或S=-
x+18(x>-8)或S=-![]() x-18(x<-8),
x-18(x<-8),
或写成S=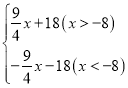 ;
;
(2)当S=![]() x+18(x>-8),△OAP的面积为
x+18(x>-8),△OAP的面积为![]() ,
,
∴![]() x+18=
x+18=![]() ,解得x=-2,代入
,解得x=-2,代入![]() ,得y=
,得y=![]() ,
,
∴P(-2,![]() )
)
当S=-![]() x-18(x<-8),△OAP的面积为
x-18(x<-8),△OAP的面积为![]() ,
,
∴-![]() x-18=
x-18=![]() ,解得x=-14,代入
,解得x=-14,代入![]() ,得y=
,得y=![]() ,
,
∴P(-14,![]() )
)
综上所述,点P的坐标为P(-2,![]() )或(-14,
)或(-14,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象如图所示,则在“①
的图象如图所示,则在“① ,②
,② ,③
,③ ,④
,④ ”中正确的判断是( )
”中正确的判断是( )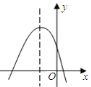
A. ①②③④ B. ④ C. ①②③ D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于点Q,PQ=3,PE=1.
(1)求证:∠ABE=∠CAD;
(2)求BP和AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进
 、
、 两种新型节能台灯共
两种新型节能台灯共 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:
(
 )若商场预计进货款为
)若商场预计进货款为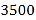 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?(
 )若商场规定
)若商场规定 型台灯的进货数量不超过
型台灯的进货数量不超过 型台灯数量的
型台灯数量的 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以
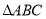 的边
的边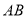 ,
, 所在直线为对称轴作
所在直线为对称轴作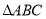 的对称图形
的对称图形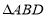 和
和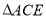 ,
, ,线段
,线段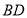 与
与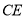 相交于点
相交于点 ,连接
,连接 、
、 、
、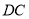 、
、 .有如下结论:①
.有如下结论:①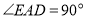 ;②
;② ;③
;③ 平分
平分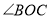 ;其中正确的结论个数是( )
;其中正确的结论个数是( )
A.0个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
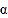 ,
,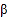 是关于
是关于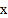 的方程
的方程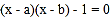 的两实根,实数
的两实根,实数 、
、 、
、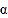 、
、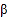 的大小关系可能是( )
的大小关系可能是( )A. α<a<b<β B. a<α<β<b C. a<α<b<β D. α<a<β<b
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小亮同学设计的一个轴对称图形的一部分.其中点
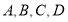 都在直角坐标系网格的格点上,每个小正方形的边长都等于1.
都在直角坐标系网格的格点上,每个小正方形的边长都等于1.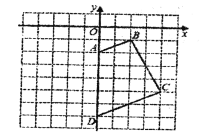
(1)请画出关于
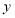 轴成轴对称图形的另一半,并写出
轴成轴对称图形的另一半,并写出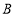 ,
,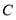 两点的对应点坐标.
两点的对应点坐标.(2)记
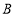 ,
,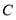 两点的对应点分别为
两点的对应点分别为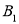 ,
, ,请直接写出封闭图形
,请直接写出封闭图形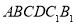 的面积.
的面积.
相关试题

