【题目】如图,在△ABC中,AD是角平分线,AE是高,已知∠BAC=2∠B,∠B=2∠DAE,那么∠ACB的度数为.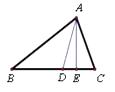
参考答案:
【答案】72°
【解析】∵AE是高,
∴∠AED=∠AEC=90°,
又∵AD是角平分线,
∴∠BAD=∠CAD=![]() ∠BAC,
∠BAC,
∴∠DAE=∠DAC-∠CAE=![]() ∠BAC-(90°-∠ACB),
∠BAC-(90°-∠ACB),
又∵∠BAC=2∠B,
∴∠BAC+∠B+∠ACB=180°,
∴∠ACB=180°-3∠B,
又∵∠B=2∠DAE,
∴∠DAE=![]() ∠B,
∠B,
∴![]() ∠B=
∠B=![]() ×2∠B-【90°-(180°-3∠B)】,
×2∠B-【90°-(180°-3∠B)】,
∴∠B=36°,
∴∠ACB=180°-3×36°=72°,
所以答案是:72°.
【考点精析】根据题目的已知条件,利用角的平分线和三角形的内角和外角的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
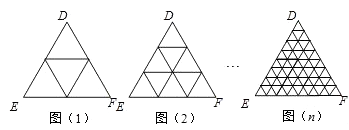
查看答案和解析>>【题目】一个三角形两边中点的连线叫做这个三角形的中位线.只要顺次连结三角形三条中位线,则可将原三角形分割为四个全等的小三角形(如图(1));把三条边分成三等份,再按照图(2)将分点连起来,可以看作将整个三角形分成9个全等的小三角形;把三条边分成四等份,…,按照这种方式分下去,第n个图形中应该得到( )个全等的小三角形.
A.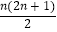
B.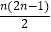
C.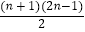
D.(n+1)2 -
科目: 来源: 题型:
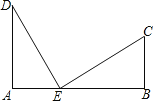
查看答案和解析>>【题目】如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x﹣1=0,②
 x+1=0,③x﹣(3x+1)=﹣5中,不等式组
x+1=0,③x﹣(3x+1)=﹣5中,不等式组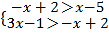 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)(2)若不等式组
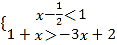 的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)(3)若方程3﹣x=2x,3+x=2(x+
 )都是关于x的不等式组
)都是关于x的不等式组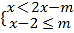 的关联方程,直接写出m的取值范围.
的关联方程,直接写出m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,四边形ABCD的顶点都在格点上.
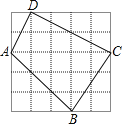
(1)求四边形ABCD的周长;
(2)连接AC,试判断△ACD的形状,并说明理由.
-
科目: 来源: 题型:
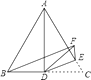
查看答案和解析>>【题目】如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,且∠CDE=20°,现将△CDE沿直线DE折叠得到△FDE,连结BF.∠BFE的度数是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABD中,AD=BD,点F是AD上的一个动点,过点A作AC⊥BF,交BF的延长线于点E,交BD的延长线于点C,则下列说法错误的是( )
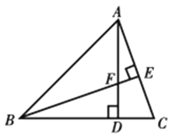
A.CD=DFB.AC=BFC.AD=BED.∠CAD+∠ABF=45°
相关试题

