【题目】如图,在等腰直角三角形ABD中,AD=BD,点F是AD上的一个动点,过点A作AC⊥BF,交BF的延长线于点E,交BD的延长线于点C,则下列说法错误的是( )
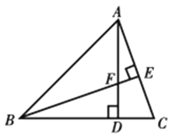
A.CD=DFB.AC=BFC.AD=BED.∠CAD+∠ABF=45°
参考答案:
【答案】C
【解析】
由余角的性质可得∠CAD=∠CBE,然后根据ASA即可证明△ADC≌△BDF,进而可判断A、B两项,由AD=BD<BF<BE即可判断C项,由∠CAD+∠ABF=∠CBE+∠ABF=∠ABD即可判断D选项,进而可得答案.
解:∵AD⊥BC,AC⊥BE,
∴∠ADB=∠ADC=90°,∠C+∠CAD=90°,∠C+∠CBE=90°,
∴∠CAD=∠CBE,
又∵AD=BD,
∴△ADC≌△BDF(ASA),
∴CD=DF,AC=BF,∴A、B两选项是正确的;
∵AD=BD<BF<BE,∴C选项是错误的;
∵△ABD是等腰直角三角形,
∴∠ABD=45°,
∴∠CAD+∠ABF=∠CBE+∠ABF=45°,∴选项D是正确的.
故选:C.
-
科目: 来源: 题型:
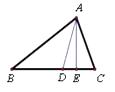
查看答案和解析>>【题目】如图,在△ABC中,AD是角平分线,AE是高,已知∠BAC=2∠B,∠B=2∠DAE,那么∠ACB的度数为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,四边形ABCD的顶点都在格点上.
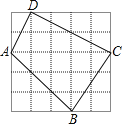
(1)求四边形ABCD的周长;
(2)连接AC,试判断△ACD的形状,并说明理由.
-
科目: 来源: 题型:
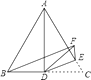
查看答案和解析>>【题目】如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,且∠CDE=20°,现将△CDE沿直线DE折叠得到△FDE,连结BF.∠BFE的度数是.
-
科目: 来源: 题型:
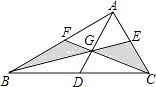
查看答案和解析>>【题目】如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数a,b,c满足|a-
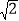 |+
|+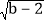 =
=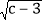 +
+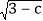 .
.(1)求a,b,c;
(2)若满足上式的a,c为等腰三角形的两边,求这个等腰三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】细心观察图形,认真分析各式,然后解答问题.
OA22=
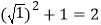 ,
, ;
;OA32=12+
 ,
, ;
;OA42=12+
 ,
, …
…(1)请用含有n(n是正整数)的等式表示上述变规律:OAn2等于多少;Sn等于多少.
(2)求出OA10的长.
(3)若一个三角形的面积是
 ,计算说明他是第几个三角形?
,计算说明他是第几个三角形?(4)求出S12+S22+S32+…+S102的值.

相关试题

