【题目】如图,在方格纸中,每个小正方形的边长为1个单位长度,正方形ABFG和FCDE的顶点均和小正方形的顶点重合.
(1)建立平面直角坐标系,使得B,C的坐标分别为(0,0),(4,0),并写出点A的坐标;
(2)直接写出正方形FCDE的边长;
(3)连接EG,直接比较三角形BCF和三角形GEF的面积大小 (用“大于”,“小于”,“等于”作答)

参考答案:
【答案】(1)见解析,A(-2,3);(2)![]() ;(3)等于
;(3)等于
【解析】
(1)利用点B和点C的坐标画出直角坐标系,然后根据点的坐标的意义即可得到点A的坐标;
(2)根据购股定理求出正方形FCDE的边长即可;
(3)分别计算出△BCF 和△GEF的面积,比较即可得出答案.
解:(1)如图,点A的坐标为:A(-2,3);
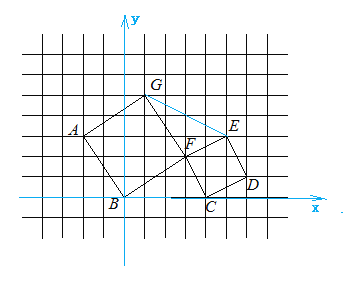
(2)正方形FCDE的边长为:![]() ;
;
(3)![]() ,
,
![]()
![]() ,
,
∴三角形BCF的面积等于三角形GEF的面积.
故答案为:(1)见解析,A(-2,3);(2)![]() ;(3)等于.
;(3)等于.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中:①有限小数是有理数;②无限小数都是无理数;③任意两个无理数的和还是无理数;④开方开不尽的数是无理数;⑤一个数的算术平方根一定是正数;⑥一个数的立方根一定比这个数小;⑦任意两个有理数之间都有有理数,任意两个无理数之间都有无理数.⑧有理数和数轴上的点一一对应;⑨不带根号的数一定是有理数;⑩负数没有立方根.其中正确的有( )
A.
 个B.
个B.  个C.
个C.  个D.
个D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在两条垂直相交的道路上,一辆自行车和一辆摩托车相遇后又分别向北向东驶去,若自行车与摩托车每秒分别行驶
 米、
米、 米,则
米,则 秒后两车相距( )米.
秒后两车相距( )米.A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某中学数学课题学习小组在“测量物体高度”的活动中,欲测量一棵古树DE的高度,他们在这棵古树的正前方一平房顶A点处测得古树顶端D的仰角为30°,在这棵古树的正前方C处,测得古树顶端D的仰角为60°,在A点处测得C点的俯角为30°.已知BC为4米,且B、C、E三点在同一条直线上.

(1)求平房AB的高度;
(2)请求出古树DE的高度(根据以上条件求解时测角器的高度忽略不计) -
科目: 来源: 题型:
查看答案和解析>>【题目】某班为奖励在小运动会上取得较好成绩的运动员,花了400元钱购买甲、乙两种奖品共30件,其中甲种奖品每件16元,乙种奖品每件12元,求甲乙两种奖品各买多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形ABC中, ∠B=60°, ∠C=
 ,点D是AB上一点,点E是AC上一点, ∠ADE=60°, 点F为线段BC上一点,连接EF,过D作DG//AC交EF于点G,
,点D是AB上一点,点E是AC上一点, ∠ADE=60°, 点F为线段BC上一点,连接EF,过D作DG//AC交EF于点G,(1)若
 =40°,求∠EDG的度数;
=40°,求∠EDG的度数;(2)若∠FEC=2∠DEF,∠DGF=
 ∠BFG,求
∠BFG,求 .
.
-
科目: 来源: 题型:
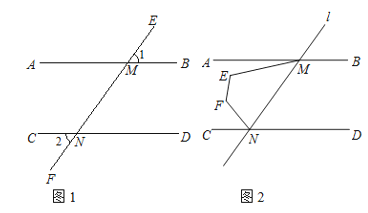
查看答案和解析>>【题目】如图,直线l分别交AB,CD于点M,N(点M在点N的右侧),若∠1=∠2
(1)求证:AB//CD;
(2)如图,点E、F在AB,CD之间,且在MN的左侧,若∠MEF+∠EFN=255°,求∠AME+∠FNC的度数;
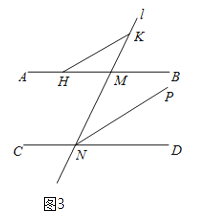
(3)如图,点H在直线AB上,且位于点M的左侧;点K在直线MN上,且在直线AB的上方.点Q在∠MND的角平分线NP上,且∠KHM=2∠MHQ,若∠HQN+∠HKN=75°,直接写出∠PND和∠QHB的数量关系.
相关试题

