【题目】如图,在三角形ABC中, ∠B=60°, ∠C=![]() ,点D是AB上一点,点E是AC上一点, ∠ADE=60°, 点F为线段BC上一点,连接EF,过D作DG//AC交EF于点G,
,点D是AB上一点,点E是AC上一点, ∠ADE=60°, 点F为线段BC上一点,连接EF,过D作DG//AC交EF于点G,
(1)若![]() =40°,求∠EDG的度数;
=40°,求∠EDG的度数;
(2)若∠FEC=2∠DEF,∠DGF=![]() ∠BFG,求
∠BFG,求![]() .
.

参考答案:
【答案】(1)40°;(2)72°
【解析】
(1)根据同位角相等即可判断出DE∥BC,根据平行线的性质即可求解;
(2)设∠DEF=x°,∠FEC=2x°,根据平行线的性质得∠DGE=∠FEC=2x° ,DEF=∠EFC=x°,分别表示出∠DGF、∠BFG,可得关于x的方程,解方程求得x的值,由三角形的内角和即可求解.
(1)∵∠B=∠ADE=60°
∴DE∥BC
∴∠C=∠AED=40°
又DG∥AC
∴∠GDE=∠AED=40°;
(2)∵∠FEC=2∠DEF
∴设∠DEF=x°,∠FEC=2x°
∵DG∥BC
∴∠DGE=∠FEC=2x°
∴∠DGF=(180-2x)°
又DE∥BC
∴∠DEF=∠EFC=x°
∴∠BFG=(180-x)°
又∠DGF=![]() ∠BFG
∠BFG
∴180-2x=![]() (180-x)
(180-x)
∴x=36,
∴∠EFC=x°=36°,∠FEC=2x°=72°,
∴∠C=α=180°-∠EFC -∠FEC =72°.
故答案为:(1)40°;(2)72°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某中学数学课题学习小组在“测量物体高度”的活动中,欲测量一棵古树DE的高度,他们在这棵古树的正前方一平房顶A点处测得古树顶端D的仰角为30°,在这棵古树的正前方C处,测得古树顶端D的仰角为60°,在A点处测得C点的俯角为30°.已知BC为4米,且B、C、E三点在同一条直线上.

(1)求平房AB的高度;
(2)请求出古树DE的高度(根据以上条件求解时测角器的高度忽略不计) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中,每个小正方形的边长为1个单位长度,正方形ABFG和FCDE的顶点均和小正方形的顶点重合.
(1)建立平面直角坐标系,使得B,C的坐标分别为(0,0),(4,0),并写出点A的坐标;
(2)直接写出正方形FCDE的边长;
(3)连接EG,直接比较三角形BCF和三角形GEF的面积大小 (用“大于”,“小于”,“等于”作答)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为奖励在小运动会上取得较好成绩的运动员,花了400元钱购买甲、乙两种奖品共30件,其中甲种奖品每件16元,乙种奖品每件12元,求甲乙两种奖品各买多少件?
-
科目: 来源: 题型:
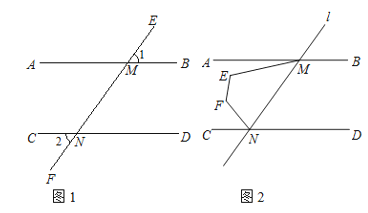
查看答案和解析>>【题目】如图,直线l分别交AB,CD于点M,N(点M在点N的右侧),若∠1=∠2
(1)求证:AB//CD;
(2)如图,点E、F在AB,CD之间,且在MN的左侧,若∠MEF+∠EFN=255°,求∠AME+∠FNC的度数;
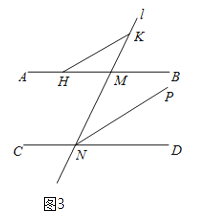
(3)如图,点H在直线AB上,且位于点M的左侧;点K在直线MN上,且在直线AB的上方.点Q在∠MND的角平分线NP上,且∠KHM=2∠MHQ,若∠HQN+∠HKN=75°,直接写出∠PND和∠QHB的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(a,1)、B(-1,b)的坐标满足:
 .
.(1)直接写出点A、B的坐标;
(2)如图,过点E(m,0)(m>1)作x轴的垂线l1,点A关于l1的对称点为A’(2m-1,1),若BA’交x轴于点F,当E点在x轴上运动时,求EF的长度;
(3)如图,把点A向上平移2个单位到点C,过点C作y轴的垂线l2,点D(n,c)在直线l2上(不和C重合),若∠CDA=
 ,连接OA、DA,∠AOx=45°,若满足∠DAO=225°-
,连接OA、DA,∠AOx=45°,若满足∠DAO=225°- ,求n的取值范围.
,求n的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.
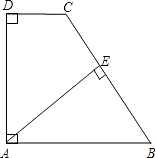
(1)求证:AD=AE;
(2)若AD=8,DC=4,求AB的长.
相关试题

