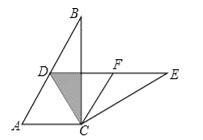
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按照顺时针方向旋转m度后得到△DEC,点D刚好落在AB边上.
(1)求m的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
参考答案:
【答案】(1)60;(2)菱形.
【解析】试题分析:(1)首先证明∠A=60°,AC=DC,判断△DAC为等边三角形,得到∠ACD=60°,即可解决问题.
(2)根据题意,证明AD=AC;再证明DF=CF=AD,得到AD=DF=CF=AC,即可解决问题.
试题解析:解:(1)如图,∵∠ACB=90°,∠B=30°,∴AB=2AC,∠A=60°.
由题意得:AC=DC,∴△DAC为等边三角形,∴∠ACD=60°,∴m=60°;
(2)∵△DAC为等边三角形,∴AD=AC.∵AB=AD+BD=2AC,∴AD =BD=![]() AB,
AB,
由题意得:DE=AB,∠DCE=∠ACB=90°.
∵F是DE的中点,∴DF=CF=![]() DE=
DE=![]() AB,∴AD=DF=CF=AC,∴四边形ACFD为菱形.
AB,∴AD=DF=CF=AC,∴四边形ACFD为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1所示,△ABC中,∠ACB的角平分线CF与∠EAC的角平分线AD的反向延长线交于点F;
①若∠B=90°则∠F= ;
②若∠B=a,求∠F的度数(用a表示);
(2)如图2所示,若点G是CB延长线上任意一动点,连接AG,∠AGB与∠GAB的角平分线交于点H,随着点G的运动,∠F+∠H的值是否变化?若变化,请说明理由;若不变,请求出其值.

-
科目: 来源: 题型:
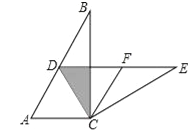
查看答案和解析>>【题目】以四边形ABCD的边AB,AD为边分别向外侧作等边△ABF和等边△ADE,连接EB,FD,交点为G.
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由.
-
科目: 来源: 题型:
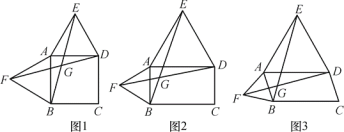
查看答案和解析>>【题目】如图,均为7×6的正方形网格,点A、B、C均在格点(小正方形的顶点)上,在图中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其满足下列条件(三个图形互不相同):
(1)在图①中所画的四边形中,∠D为钝角,且四边形是轴对称图形.
(2)在图②中所画的四边形中,∠D为锐角,且四边形是中心对称图形.
(3)在图③所画的四边形中,∠D为直角,且四边形面积为5平方单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 过平行四边形
过平行四边形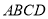 对角线的交点
对角线的交点 ,分别交
,分别交 、
、 于
于 、
、 ,那么阴影部分的面积是平行四边形
,那么阴影部分的面积是平行四边形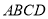 面积的( )
面积的( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一副三角板的三个内角分别是
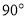 ,
,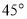 ,
,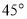 和
和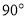 ,
,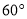 ,
,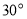 ,按如图所示叠放在一起(点
,按如图所示叠放在一起(点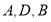 在同一直线上),若固定
在同一直线上),若固定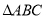 ,将
,将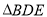 绕着公共顶点
绕着公共顶点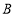 顺时针旋转
顺时针旋转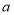 度(
度(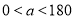 ),当边
),当边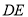 与
与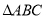 的某一边平行时,相应的旋转角
的某一边平行时,相应的旋转角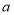 的值为_______.
的值为_______.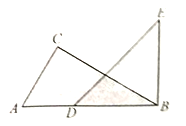
相关试题

