【题目】 
(1)如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.
(2)植树节期间,两所学校共植树834棵,其中海石中学植树的数量比励东中学的2倍少3棵,两校各植树多少棵?
参考答案:
【答案】
(1)证明:∵AB⊥BD,ED⊥BD
∴∠ABC=∠D=90°,
在△ABC和△EDC中  ,
,
∴△ABC≌△EDC,
∴AB=ED
(2)解:设励东中学植树x棵,
依题意,得x+(2x﹣3)=834,
解得x=279,
∴2x﹣3=2×279﹣3=555,
答:励东中学植树279棵,海石中学植树555棵
【解析】(1)根据已知条件可判断出△ABC≌△EDC,根据全等三角形的性质即可得出AB=ED,(2)设励东中学植树x棵,可知海石中学植树2x﹣3颗,根据题意列出方程,解出x的值,即可得出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.
如图,抛物线y=x2﹣2x﹣3与x轴交于点A,B,与y轴交于点D,以AB为直径,在x轴上方作半圆交y轴于点C,半圆的圆心记为M,此时这个半圆与这条抛物线x轴下方部分组成的图形就称为“蛋圆”.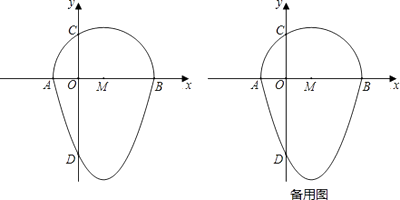
(1)直接写出点A,B,C的坐标及“蛋圆”弦CD的长;
A , B , C , CD=;
(2)如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.
①求经过点C的“蛋圆”切线的解析式;
②求经过点D的“蛋圆”切线的解析式;
(3)由(2)求得过点D的“蛋圆”切线与x轴交点记为E,点F是“蛋圆”上一动点,试问是否存在S△CDE=S△CDF , 若存在请求出点F的坐标;若不存在,请说明理由;
(4)点P是“蛋圆”外一点,且满足∠BPC=60°,当BP最大时,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列单项式:
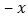 ,
,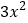 ,
,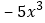 ,
,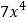 ,…
,…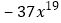 ,
,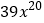 ,…写出第
,…写出第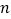 个单项式,为了解这个问题,特提供下面的解题思路.
个单项式,为了解这个问题,特提供下面的解题思路. 这组单项式的系数的符号,绝对值规律是什么?
这组单项式的系数的符号,绝对值规律是什么? 这组单项式的次数的规律是什么?
这组单项式的次数的规律是什么? 根据上面的归纳,你可以猜想出第
根据上面的归纳,你可以猜想出第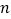 个单项式是什么?
个单项式是什么? 请你根据猜想,请写出第
请你根据猜想,请写出第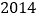 个,第
个,第 个单项式.
个单项式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在Rt ΔABC中,∠ABC=900, AB=BC=2.
(1)用尺规作∠A的平分线AD.
(2)角平分线AD交BC于点D,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了绿化校园,我校决定修建一块长方形草坪,长
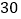 米,宽
米,宽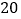 米,并在草坪上修建如图所示的十字路,设小路的宽为
米,并在草坪上修建如图所示的十字路,设小路的宽为 米.
米.
 用含
用含 的式子分别表示出草坪的面积、小路的面积;
的式子分别表示出草坪的面积、小路的面积; 写出
写出 中多项式的项、次数,并说明是几次几项式?
中多项式的项、次数,并说明是几次几项式? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一份汽车票价表,李丽星期一、三、五要乘汽车上下班,星期二、四乘汽车上班,而搭朋友的车回家;她应该买什么样的票合算?如果周末她要乘汽车去公园,那么她选哪种票合算?
汽车公司票价表
单程票
 元
元周票
 元
元 -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道
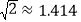 ,于是我们说:“
,于是我们说:“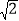 的整数部分为
的整数部分为 ,小数部分则可记为
,小数部分则可记为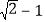 ”.则:
”.则:(1)
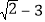 的整数部分为________,小数部分则可记为________;
的整数部分为________,小数部分则可记为________;(2)已知
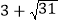 的小数部分为
的小数部分为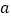 ,
,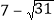 的小数部分为
的小数部分为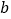 ,那么
,那么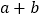 的值是________;
的值是________;(3)已知
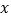 是
是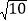 的整数部分,
的整数部分,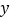 是
是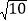 的小数部分,求
的小数部分,求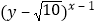 的平方根.
的平方根.
相关试题

