【题目】综合题
(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,试探索∠1+∠2与∠A的关系.(不必证明). 
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数; 
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论. 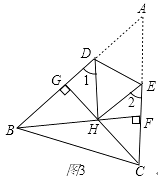
参考答案:
【答案】
(1)解:∠1+∠2=2∠A
(2)解:由(1)∠1+∠2=2∠A,得2∠A=130°,∴∠A=65°
∵IB平分∠ABC,IC平分∠ACB,
∴∠IBC+∠ICB= ![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
= ![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣ ![]() ∠A,
∠A,
∴∠BIC=180°﹣(∠IBC+∠ICB),
=180°﹣(90°﹣ ![]() ∠A)=90°+
∠A)=90°+ ![]() ×65°=122.5°
×65°=122.5°
(3)解:∵BF⊥AC,CG⊥AB,∴∠AFH+∠AGH=90°+90°=180°,
∠FHG+∠A=180°,∴∠BHC=∠FHG=180°﹣∠A,由(1)知∠1+∠2=2∠A,
∴∠A= ![]() (∠1+∠2),
(∠1+∠2),
∴∠BHC=180°﹣ ![]() (∠1+∠2)
(∠1+∠2)
【解析】(1)根据翻折变换的性质以及三角形内角和定理以及平角的定义求出即可;(2)根据三角形角平分线的性质得出∠IBC+∠ICB=90°﹣ ![]() ∠A,得出∠BIC的度数即可;(3)根据翻折变换的性质以及垂线的性质得出,∠AFH+∠AGH=90°+90°=180°,进而求出∠A=
∠A,得出∠BIC的度数即可;(3)根据翻折变换的性质以及垂线的性质得出,∠AFH+∠AGH=90°+90°=180°,进而求出∠A= ![]() (∠1+∠2),即可得出答案.
(∠1+∠2),即可得出答案.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
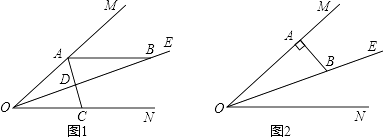
(1)如图1,若AB∥ON,则
①∠ABO的度数是;
②当∠BAD=∠ABD时,x=;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN,sin∠EMP=
 .
.(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A、C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出x的取值范围;
(3)若△AME∽△ENB,求AP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】3a2-5a+1与-2a2-3a-4的和为( )
A. 5a2-2a-3 B. a2-8a-3 C. -a2-3a-5 D. a2-8a+5
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2013年四川广安3分)等腰三角形的一条边长为6,另一边长为13,则它的周长为【 】
A.25 B.25或32 C.32 D.19
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M是线段AC的中点,N是线段BC的中点.

(1)如果AC=8cm,BC=6cm,求MN的长.
(2)如果AM=5cm,CN=2cm,求线段AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆客房有三人客房、双人客房,收费数据如下表:

为吸引游客,实行团体入住五折优惠措施,一个50人的旅游团优惠期间到该宾馆入住,住了若干间三人普通间客房和双人普通房间客房。若每间客房正好住满,且一天共花去住宿费1510元,则旅游团住了三人普通间和双人普通间客房各多少间?
相关试题

