【题目】在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN,sin∠EMP=![]() .
.
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A、C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出x的取值范围;
(3)若△AME∽△ENB,求AP的长.

参考答案:
【答案】(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)
[解] (1) 由AE=40,BC=30,AB=50,CP=24,又sinEMP=![]() CM=26。
CM=26。
(2) 在Rt△AEP與Rt△ABC中,∵EAP=BAC,∴ Rt△AEP~ Rt△ABC,
∴![]() ,即
,即![]() ,∴EP=
,∴EP=![]() x,
x,
又sinEMP=![]() tgEMP=
tgEMP=![]() =
=![]()
![]() =
=![]() ,∴MP=
,∴MP=![]() x=PN,
x=PN,
BN=AB-AP-PN=50-x-![]() x=50-
x=50-![]() x(0<x<32)。
x(0<x<32)。
(3) j當E在線段AC上時,由(2)知,![]() ,即
,即 ,EM=
,EM=![]() x=EN,
x=EN,
又AM=AP-MP=x-![]() x=
x=![]() x,
x,
由題設△AME~ △ENB,∴![]() ,
,![]() =
= ,解得x=22=AP。
,解得x=22=AP。
k當E在線段BC上時,由題設△AME~ △ENB,∴AEM=EBN
由外角定理,AEC=EAB+EBN=EAB+AEM=EMP,
∴Rt△ACE~Rt△EPM,![]() ,即
,即 ,CE=
,CE=![]() …j。
…j。
設AP=z,∴PB=50-z,
由Rt△BEP~Rt△BAC,![]() ,即
,即![]() =
=![]() ,BE=
,BE=![]() (50-z),∴CE=BC-BE=30-
(50-z),∴CE=BC-BE=30-![]() (50-z)…k。
(50-z)…k。
由j,k,解![]() =30-
=30-![]() (50-z),得z=42=AP。
(50-z),得z=42=AP。
【解析】略
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)
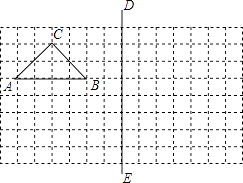
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点P,使PB1+PC最小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个角互补,那么这两个角可能是
①均为直角;②均为钝角;③一个为锐角,一个为钝角;④以上三者都有可能
A. ①② B. ①③ C. ②③ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
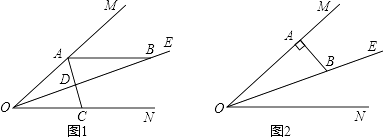
(1)如图1,若AB∥ON,则
①∠ABO的度数是;
②当∠BAD=∠ABD时,x=;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】3a2-5a+1与-2a2-3a-4的和为( )
A. 5a2-2a-3 B. a2-8a-3 C. -a2-3a-5 D. a2-8a+5
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,试探索∠1+∠2与∠A的关系.(不必证明).
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数;
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.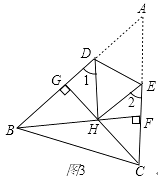
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2013年四川广安3分)等腰三角形的一条边长为6,另一边长为13,则它的周长为【 】
A.25 B.25或32 C.32 D.19
相关试题

