【题目】如图,等腰Rt△ABC中,∠ABC=90°,AB=BC,点A,B分别在坐标轴上.
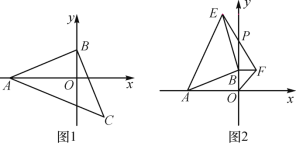
(1)如图1,若点C的横坐标为5,直接写出点B的坐标 ;
(2)如图2,若点A的坐标为(-6,0),点B在y轴的正半轴上运动时,分别以OB,AB为边在第一、第二象限作等腰Rt△OBF,等腰Rt△ABE,连接EF交y轴于点P,当点B在y轴的正半轴上移动时,PB的长度是否发生改变?若不变,求出PB的值;若变化,求PB的取值范围.
参考答案:
【答案】(1) (0,5);(2)不变,PB=3,理由见解析
【解析】
(1)作CD⊥BO,易证△ABO≌△BCD,根据全等三角形对应边相等的性质即可解题;
(2)作EG⊥y轴,易证△BAO≌△EBG和△EGP≌△FBP,可得BG=AO和PB=PG,即可求得PB![]() AO,即可解题.
AO,即可解题.
(1)如图1,作CD⊥BO于D.
∵∠CBD+∠ABO=90°,∠ABO+∠BAO=90°,∴∠CBD=∠BAO,
在△ABO和△BCD中,∵ ,
,
∴△ABO≌△BCD(AAS),∴CD=BO=5,∴B点坐标(0,5).
故答案为:(0,5);
(2)如图3,作EG⊥y轴于G.
∵∠BAO+∠OBA=90°,∠OBA+∠EBG=90°,∴∠BAO=∠EBG,
在△BAO和△EBG中,∵ ,
,
∴△BAO≌△EBG(AAS),∴BG=AO,EG=OB.
∵OB=BF,∴BF=EG,
在△EGP和△FBP中,∵ ,
,
∴△EGP≌△FBP(AAS),∴PB=PG,∴PB![]() BG
BG![]() AO=3.
AO=3.


-
科目: 来源: 题型:
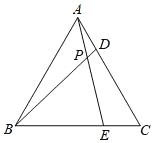
查看答案和解析>>【题目】如图,△ABC 为等边三角形,D、E 分别是边 AC、BC 上的点,且AD=CE,AE 与 BD 相交于点 P.
(1)求∠BPE 的度数;
(2)若 BF⊥AE 于点 F,试判断 BP 与 PF 的数量关系并说明理由.
-
科目: 来源: 题型:
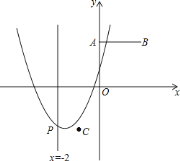
查看答案和解析>>【题目】如图,已知点
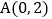 ,
,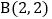 ,
,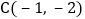 ,抛物线
,抛物线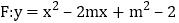 与直线
与直线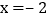 交于点
交于点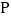 .
.
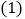 当抛物线
当抛物线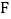 经过点
经过点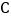 时,求它的表达式;
时,求它的表达式;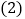 设点
设点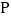 的纵坐标为
的纵坐标为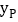 ,求
,求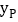 的最小值,此时抛物线
的最小值,此时抛物线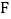 上有两点
上有两点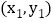 ,
,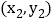 ,且
,且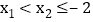 ,比较
,比较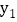 与
与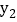 的大小;
的大小; 当抛物线
当抛物线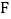 与线段
与线段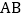 有公共点时,直接写出
有公共点时,直接写出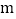 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于
 的一元二次方程
的一元二次方程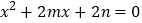 有两个整数根且乘积为正,关于
有两个整数根且乘积为正,关于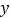 的一元二次方程
的一元二次方程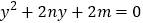 同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②
同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;② ;③
;③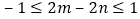 ,其中正确结论的个数是( )
,其中正确结论的个数是( )A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
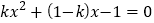 ,下列说法正确的是( )
,下列说法正确的是( )A. 当k=0时,方程没有实数根 B. 当k=1时,方程有一个实数根
C. 当k=-1时,方程有两个相等的实数根 D. 当k≠0时,方程总有两个不相等的实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°,AB=2,BC=1,CD=2,AD=3,连接AC.
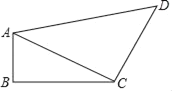
(1)求AC的长;
(2)判断三角形ACD的形状,并求出四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
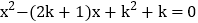 。
。(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
相关试题

