【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个整数根且乘积为正,关于
有两个整数根且乘积为正,关于![]() 的一元二次方程
的一元二次方程![]() 同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②
同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②![]() ;③
;③![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 0个 B. 1个 C. 2个 D. 3个
参考答案:
【答案】D
【解析】
设方程![]() 的两根为x1、x2,方程
的两根为x1、x2,方程![]() 同的两根为y1、y2.①根据方程解的情况可得出x1x2=2n>0、y1y2=2m>0,结合根与系数的关系可得出x1+x2=-2m、y1+y2=-2n,进而得出这两个方程的根都是负根,①正确;②由方程有两个实数根结合根的判别式即可得出m2-2n≥0、n2-2m≥0,将(m-1)2+(n-1)2展开代入即可得出②正确;③根据根与系数的关系可得出2m-2n=(y1+1)(y2+1)-1、2n-2m=(x1+1)(x2+1)-1,结合x1、x2、y1、y2均为负整数即可得出-1≤2m-2n≤1,③成立.综上即可得出结论.
同的两根为y1、y2.①根据方程解的情况可得出x1x2=2n>0、y1y2=2m>0,结合根与系数的关系可得出x1+x2=-2m、y1+y2=-2n,进而得出这两个方程的根都是负根,①正确;②由方程有两个实数根结合根的判别式即可得出m2-2n≥0、n2-2m≥0,将(m-1)2+(n-1)2展开代入即可得出②正确;③根据根与系数的关系可得出2m-2n=(y1+1)(y2+1)-1、2n-2m=(x1+1)(x2+1)-1,结合x1、x2、y1、y2均为负整数即可得出-1≤2m-2n≤1,③成立.综上即可得出结论.
设方程![]() 的两根为x1、x2,方程
的两根为x1、x2,方程![]() 同的两根为y1、y2.
同的两根为y1、y2.
①∵关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正,
∴x1x2=2n>0,y1y2=2m>0,
∵x1+x2=-2m,y1+y2=-2n,
∴这两个方程的根都是负根,①正确;
②∵关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正,
∴4m2-8n≥0,4n2-8m≥0,
∴m2-2n≥0,n2-2m≥0,
∴(m-1)2+(n-1)2=m2-2n+1+n2-2m+1≥2,②正确;
③∵y1y2=2m,y1+y2=-2n,
∴2m-2n=y1y2+y1+y2=(y1+1)(y2+1)-1,
∵y1、y2均为负整数,
∴(y1+1)(y2+1)≥0,
∴2m-2n≥-1.
∵x1x2=2n,x1+x2=-2m,
∴2n-2m=x1x2+x1+x2=(x1+1)(x2+1)-1,
∵x1、x2均为负整数,
∴(x1+1)(x2+1)≥0,
∴2 n -2 m≥-1,即2m-2n≤1.
∴-1≤2m-2n≤1,③成立.
综上所述:成立的结论有①②③.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,分别以点A和点B为圆心,大于
 AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
-
科目: 来源: 题型:
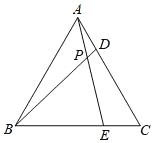
查看答案和解析>>【题目】如图,△ABC 为等边三角形,D、E 分别是边 AC、BC 上的点,且AD=CE,AE 与 BD 相交于点 P.
(1)求∠BPE 的度数;
(2)若 BF⊥AE 于点 F,试判断 BP 与 PF 的数量关系并说明理由.
-
科目: 来源: 题型:
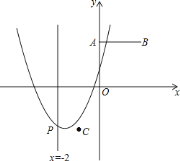
查看答案和解析>>【题目】如图,已知点
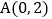 ,
,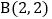 ,
,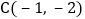 ,抛物线
,抛物线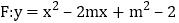 与直线
与直线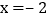 交于点
交于点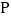 .
.
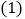 当抛物线
当抛物线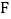 经过点
经过点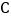 时,求它的表达式;
时,求它的表达式;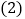 设点
设点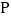 的纵坐标为
的纵坐标为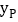 ,求
,求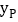 的最小值,此时抛物线
的最小值,此时抛物线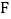 上有两点
上有两点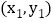 ,
,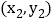 ,且
,且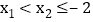 ,比较
,比较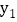 与
与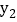 的大小;
的大小; 当抛物线
当抛物线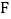 与线段
与线段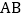 有公共点时,直接写出
有公共点时,直接写出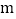 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠ABC=90°,AB=BC,点A,B分别在坐标轴上.
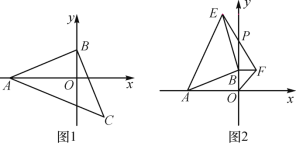
(1)如图1,若点C的横坐标为5,直接写出点B的坐标 ;
(2)如图2,若点A的坐标为(-6,0),点B在y轴的正半轴上运动时,分别以OB,AB为边在第一、第二象限作等腰Rt△OBF,等腰Rt△ABE,连接EF交y轴于点P,当点B在y轴的正半轴上移动时,PB的长度是否发生改变?若不变,求出PB的值;若变化,求PB的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
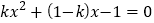 ,下列说法正确的是( )
,下列说法正确的是( )A. 当k=0时,方程没有实数根 B. 当k=1时,方程有一个实数根
C. 当k=-1时,方程有两个相等的实数根 D. 当k≠0时,方程总有两个不相等的实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°,AB=2,BC=1,CD=2,AD=3,连接AC.
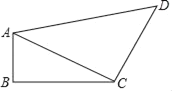
(1)求AC的长;
(2)判断三角形ACD的形状,并求出四边形ABCD的面积.
相关试题

