【题目】如图,四边形ABCD中,∠B=90°,AB=2,BC=1,CD=2,AD=3,连接AC.
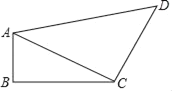
(1)求AC的长;
(2)判断三角形ACD的形状,并求出四边形ABCD的面积.
参考答案:
【答案】(1)AC=![]() ;(2)1+
;(2)1+![]() .
.
【解析】
(1)在Rt△ABC,利用勾股定理计算斜边即可.
(2)在△ACD中,利用勾股定理验证得出△ACD为直角三角形,再计算面积.
解:(1)∵∠B=90°,AB=2,BC=1,
∴AC2=AB2+BC2=4+1=5,
∴AC=![]() ;
;
(2)∵△ACD中,AC=![]() ,CD=2,AD=3,
,CD=2,AD=3,
∴AC2+CD2=5+4=9,AD2=9,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,
∴四边形ABCD的面积=1×2÷2+2×![]() ÷2=1+
÷2=1+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于
 的一元二次方程
的一元二次方程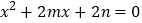 有两个整数根且乘积为正,关于
有两个整数根且乘积为正,关于 的一元二次方程
的一元二次方程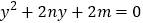 同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②
同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;② ;③
;③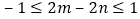 ,其中正确结论的个数是( )
,其中正确结论的个数是( )A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠ABC=90°,AB=BC,点A,B分别在坐标轴上.
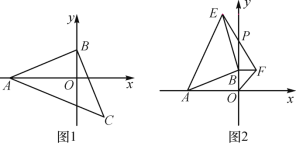
(1)如图1,若点C的横坐标为5,直接写出点B的坐标 ;
(2)如图2,若点A的坐标为(-6,0),点B在y轴的正半轴上运动时,分别以OB,AB为边在第一、第二象限作等腰Rt△OBF,等腰Rt△ABE,连接EF交y轴于点P,当点B在y轴的正半轴上移动时,PB的长度是否发生改变?若不变,求出PB的值;若变化,求PB的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
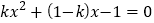 ,下列说法正确的是( )
,下列说法正确的是( )A. 当k=0时,方程没有实数根 B. 当k=1时,方程有一个实数根
C. 当k=-1时,方程有两个相等的实数根 D. 当k≠0时,方程总有两个不相等的实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
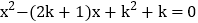 。
。(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,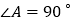 ,
,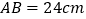 ,
,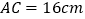 ,现有动点
,现有动点 从点
从点 出发,沿射线
出发,沿射线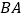 方向运动,动点
方向运动,动点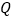 从点
从点 出发,沿射线
出发,沿射线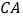 方向运动,已知点
方向运动,已知点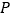 的速度是
的速度是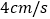 ,点
,点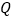 的速度是
的速度是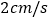 ,它们同时出发,经过________秒,
,它们同时出发,经过________秒,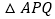 的面积是
的面积是 面积的一半?
面积的一半?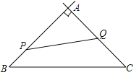
-
科目: 来源: 题型:
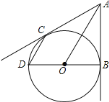
查看答案和解析>>【题目】如图,从
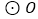 外一点
外一点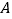 作
作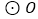 的切线
的切线 ,
,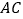 ,切点分别为
,切点分别为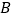 ,
,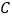 ,
,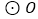 的直径
的直径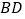 为
为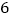 ,连结
,连结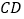 ,
,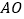 .
.
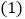 求证:
求证: ;
;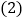 求
求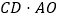 的值;
的值;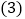 若
若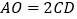 ,求劣弧
,求劣弧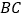 的长.
的长.
相关试题

