【题目】如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为 . 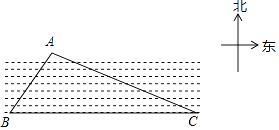
参考答案:
【答案】20 ![]() 米
米
【解析】方法1、过点A作AD⊥BC于点D.
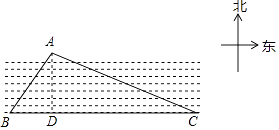
根据题意,∠ABC=90°﹣30°=60°,∠ACD=30°,
设AD=x米,
在Rt△ACD中,tan∠ACD= ![]() ,
,
∴CD= ![]() =
= ![]() =
= ![]() x,
x,
在Rt△ABD中,tan∠ABC= ![]() ,
,
∴BD= ![]() =
= ![]() =
= ![]() x,
x,
∴BC=CD+BD= ![]() x+
x+ ![]() x=80
x=80
∴x=20 ![]()
答:该河段的宽度为20 ![]() 米.
米.
故答案是:20 ![]() 米.
米.
方法2、过点A作AD⊥BC于点D.
根据题意,∠ABC=90°﹣30°=60°,∠ACD=30°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=90°,
在Rt△ABC中,BC=80m,∠ACB=30°,
∴AB=40m,AC=40 ![]() m,
m,
∴S△ABC= ![]() AB×AC=
AB×AC= ![]() ×40×40
×40×40 ![]() =800
=800 ![]() ,
,
∵S△ABC= ![]() BC×AD=
BC×AD= ![]() ×80×AD=40AD=800
×80×AD=40AD=800 ![]() ,
,
∴AD=20 ![]() 米
米
答:该河段的宽度为20 ![]() 米.
米.
故答案是:20 ![]() 米.
米.
【考点精析】根据题目的已知条件,利用三角形的面积和锐角三角函数的定义的相关知识可以得到问题的答案,需要掌握三角形的面积=1/2×底×高;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系中有一点
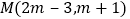 .
.(1)点M到y轴的距离为1时,M的坐标?
(2)点
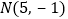 且MN//x轴时,M的坐标?
且MN//x轴时,M的坐标? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.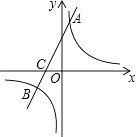
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,点D与点B在AC同侧,∠DAC>∠BAC,且DA=DC,过点B作BE∥DA交DC于点E,过E作EM∥AC交AB于点M,连结MD.
(1)当∠ADC=80°时,求∠CBE的度数.
(2)当∠ADC=α时:
①求证:BE=CE.
②求证:∠ADM=∠CDM.
③当α为多少度时,DM=
 EM.
EM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线
 :
: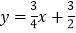 与
与 轴交于点A,且经过点B(2,m),点C(3,0).
轴交于点A,且经过点B(2,m),点C(3,0).(1)求直线BC的函数解析式;
(2)在线段BC上找一点D,使得△ABO与△ABD的面积相等,求出点D的坐标;
(3)y轴上有一动点P,直线BC上有一动点M,若△APM是以线段AM为斜边的等腰直角三角形,求出点M的坐标;
(4)如图2,E为线段AC上一点,连结BE,一动点F从点B出发,沿线段BE以每秒1个单位运动到点E,再沿线段EA以每秒
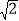 个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值. 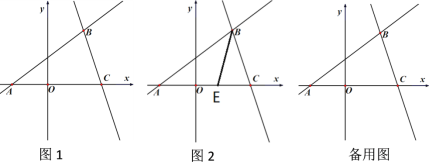
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BAC中,∠B和∠C的平分线相交于点F,过点F作DE∥BC交AB于点D,交AC于点E,若BD=5,CE=4,则线段DE的长为( )
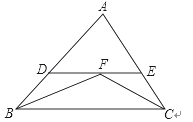
A. 9 B. 6 C. 5 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣1)2017+tan45°+
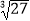 +|3﹣π|.
+|3﹣π|.
相关试题

