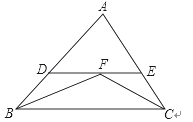
【题目】在Rt△ABC中,∠ACB=90°,点D与点B在AC同侧,∠DAC>∠BAC,且DA=DC,过点B作BE∥DA交DC于点E,过E作EM∥AC交AB于点M,连结MD.
(1)当∠ADC=80°时,求∠CBE的度数.
(2)当∠ADC=α时:
①求证:BE=CE.
②求证:∠ADM=∠CDM.
③当α为多少度时,DM=![]() EM.
EM.

参考答案:
【答案】(1)40°;(2)①见解析,②见解析,③60°
【解析】
(1)根据等腰三角形的性质可得∠ACD的度数,根据∠ACB=90°可求出∠BCE的度数,根据AD//BE可得∠BED=∠ADC=80°,根据三角形外角性质即可求出∠CBE的度数;(2)①由等腰三角形的性质可得∠ACD=90°-![]() ,根据∠ACB=90°可得∠BCE=
,根据∠ACB=90°可得∠BCE=![]() ,根据平行线性质可得∠BED=∠ADC=
,根据平行线性质可得∠BED=∠ADC=![]() ,利用外角性质可求出∠CBE=
,利用外角性质可求出∠CBE=![]() ,即可证明∠BCE=∠CBE,进而可证明BE=CE;②延长EM交AD于F,由EM∥AC可得
,即可证明∠BCE=∠CBE,进而可证明BE=CE;②延长EM交AD于F,由EM∥AC可得![]() ,进而可得DF=DE,AF=EC=BE,根据AAS可证明△AFM
,进而可得DF=DE,AF=EC=BE,根据AAS可证明△AFM![]() △BEM,可得FM=EM.,根据等腰三角形三线合一即可证明∠ADM=∠CDM;③由②可得DM⊥EM,由
△BEM,可得FM=EM.,根据等腰三角形三线合一即可证明∠ADM=∠CDM;③由②可得DM⊥EM,由![]() 可知tan∠DEM=
可知tan∠DEM=![]() ,可得∠DEM=60°,即可求出∠EDM=30°,进而可得
,可得∠DEM=60°,即可求出∠EDM=30°,进而可得![]() =∠ADC=2∠EDM=60°.
=∠ADC=2∠EDM=60°.
(1)∵AD=CD,∠ADC=80°,
∴∠ACD=![]() (180°-80°)=50°,
(180°-80°)=50°,
∵∠ACB=90°,
∴∠BCE=90°-50°=40°,
∵AD//BE,
∴∠BED=∠ADC=80°,
∴∠CBE=∠BED-∠BCE=80°-40°=40°.
(2)①![]() ,
,![]() ,
,
∴![]()
∵AD=CD,
∴∠ACD=![]() (180°-
(180°-![]() )=90°-
)=90°-![]() ,
,
∵∠ACB=90°,
∴∠BCE=90°-∠ACD=![]()
![]() ,
,
∴∠CBE=∠BED-∠BCE=![]()
![]() ,
,
∴∠CBE=∠BCE,
∴BE=CE.
②延长EM交AD于F
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AF=EC=BE
∵BE//AD,
∴∠FAM=∠EBM,∠AFM=∠BEM,
∴△AFM![]() △BEM
△BEM
∴FM=EM.
∴根据三线合一性可得∠ADM=∠CDM

③∵DF=DE,FM=EM,
∴DM⊥EM,
∵DM=![]() EM.
EM.
∴tan∠DEM=![]() =
=![]() ,
,
∴∠DEM=60°,
∴∠EDM=30°,
∴![]() =∠ADC=2∠EDM=60°.
=∠ADC=2∠EDM=60°.
-
科目: 来源: 题型:
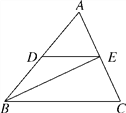
查看答案和解析>>【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系中有一点
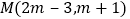 .
.(1)点M到y轴的距离为1时,M的坐标?
(2)点
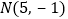 且MN//x轴时,M的坐标?
且MN//x轴时,M的坐标? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.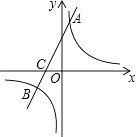
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标. -
科目: 来源: 题型:
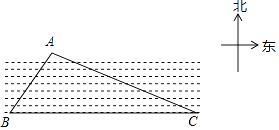
查看答案和解析>>【题目】如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线
 :
: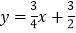 与
与 轴交于点A,且经过点B(2,m),点C(3,0).
轴交于点A,且经过点B(2,m),点C(3,0).(1)求直线BC的函数解析式;
(2)在线段BC上找一点D,使得△ABO与△ABD的面积相等,求出点D的坐标;
(3)y轴上有一动点P,直线BC上有一动点M,若△APM是以线段AM为斜边的等腰直角三角形,求出点M的坐标;
(4)如图2,E为线段AC上一点,连结BE,一动点F从点B出发,沿线段BE以每秒1个单位运动到点E,再沿线段EA以每秒
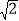 个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值. 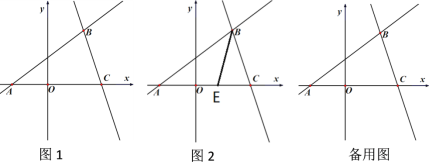
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BAC中,∠B和∠C的平分线相交于点F,过点F作DE∥BC交AB于点D,交AC于点E,若BD=5,CE=4,则线段DE的长为( )
A. 9 B. 6 C. 5 D. 4
相关试题

