搜索
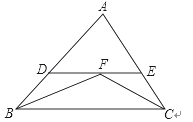
【题目】如图，在△BAC中，∠B和∠C的平分线相交于点F，过点F作DE∥BC交AB于点D，交AC于点E，若BD=5，CE=4，则线段DE的长为（ ）
A. 9 B. 6 C. 5 D. 4
参考答案：
【答案】A
【解析】
根据△ABC中，∠ABC和∠ACB的平分线相交于点F．求证∠DBF=∠FBC，∠ECF=∠BCF，再利用两直线平行内错角相等，求证出∠DFB=∠DBF，∠CFE=∠BCF，即BD=DF，FE=CE，然后利用等量代换即可求出线段DE的长．
∵∠ABC和∠ACB的平分线相交于点F，
∴∠DBF=∠FBC，∠ECF=∠BCF，
∵DE∥BC，交AB于点D，交AC于点E，
∴∠DFB=∠DBF，∠CFE=∠ECF，
∴BD=DF=5，FE=CE=4，
∴DE=DF+EF=5+4=9．
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在Rt△ABC中，∠ACB=90°，点D与点B在AC同侧，∠DAC＞∠BAC，且DA=DC，过点B作BE∥DA交DC于点E，过E作EM∥AC交AB于点M，连结MD.
（1）当∠ADC=80°时，求∠CBE的度数.
（2）当∠ADC=α时:
①求证：BE=CE.
②求证：∠ADM=∠CDM.
③当α为多少度时，DM=
EM.
-
科目： 来源： 题型：
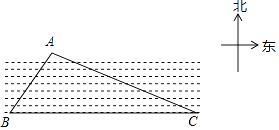
查看答案和解析>>【题目】如图，已知一条东西走向的河流，在河流对岸有一点A，小明在岸边点B处测得点A在点B的北偏东30°方向上，小明沿河岸向东走80m后到达点C，测得点A在点C的北偏西60°方向上，则点A到河岸BC的距离为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，直线
：
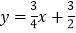与
轴交于点A，且经过点B（2，m），点C（3,0）.（1）求直线BC的函数解析式；
（2）在线段BC上找一点D，使得△ABO与△ABD的面积相等，求出点D的坐标；
（3）y轴上有一动点P，直线BC上有一动点M，若△APM是以线段AM为斜边的等腰直角三角形，求出点M的坐标；
（4）如图2，E为线段AC上一点，连结BE，一动点F从点B出发，沿线段BE以每秒1个单位运动到点E,再沿线段EA以每秒
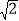个单位运动到A后停止，设点F在整个运动过程中所用时间为t，求t的最小值.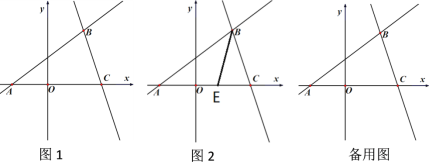 
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：（﹣1）2017+tan45°+
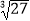+|3﹣π|． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，长方形OABC中，O为平面直角坐标系的原点，A点的坐标为（4，0），C点的坐标为（0，3），点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动（即：沿着长方形移动一周）．
（1）直接写出B点的坐标；
（2）当点P移动了3秒时，请直接写出点P的坐标；
（3）在移动过程中，当点P到x轴距离为2个单位长度时，求点P移动的时间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AE、BF、DC是直线，B在直线AC上，E在直线DF上，∠1=∠2，∠A=∠F.
求证：∠C=∠D.
证明：因为∠1=∠2（已知），∠1=∠3（ ）
得∠2=∠3（ ）
所以AE//_______( )
得∠4=∠F（ ）
因为__________(已知)
得∠4=∠A
所以______//_______( )
所以∠C=∠D( )
相关试题
