搜索
【题目】计算：（﹣1）2017+tan45°+ 
+|3﹣π|．
参考答案：
【答案】解：原式=﹣1+1+3+π﹣3
=π．
【解析】因2017为奇数，所以（﹣1）2017=-1，又因特殊角的三角函数值tan45°=1， 根据立方根的性质
=3，另任何一个数的绝对值均为正数，则|3﹣π|=π﹣3，所以原式化简后代入数值即可求解。
【考点精析】根据题目的已知条件，利用特殊角的三角函数值和实数的运算的相关知识可以得到问题的答案，需要掌握分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”；先算乘方、开方，再算乘除，最后算加减，如果有括号，先算括号里面的，若没有括号，在同一级运算中，要从左到右进行运算．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知一条东西走向的河流，在河流对岸有一点A，小明在岸边点B处测得点A在点B的北偏东30°方向上，小明沿河岸向东走80m后到达点C，测得点A在点C的北偏西60°方向上，则点A到河岸BC的距离为 ．
-
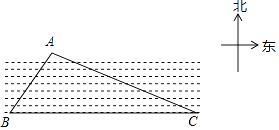
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，直线
：
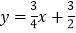与
轴交于点A，且经过点B（2，m），点C（3,0）.（1）求直线BC的函数解析式；
（2）在线段BC上找一点D，使得△ABO与△ABD的面积相等，求出点D的坐标；
（3）y轴上有一动点P，直线BC上有一动点M，若△APM是以线段AM为斜边的等腰直角三角形，求出点M的坐标；
（4）如图2，E为线段AC上一点，连结BE，一动点F从点B出发，沿线段BE以每秒1个单位运动到点E,再沿线段EA以每秒
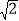个单位运动到A后停止，设点F在整个运动过程中所用时间为t，求t的最小值.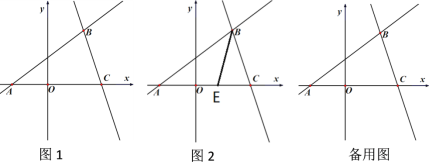 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△BAC中，∠B和∠C的平分线相交于点F，过点F作DE∥BC交AB于点D，交AC于点E，若BD=5，CE=4，则线段DE的长为（ ）
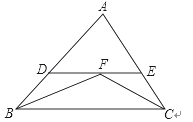
A. 9 B. 6 C. 5 D. 4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，长方形OABC中，O为平面直角坐标系的原点，A点的坐标为（4，0），C点的坐标为（0，3），点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动（即：沿着长方形移动一周）．
（1）直接写出B点的坐标；
（2）当点P移动了3秒时，请直接写出点P的坐标；
（3）在移动过程中，当点P到x轴距离为2个单位长度时，求点P移动的时间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AE、BF、DC是直线，B在直线AC上，E在直线DF上，∠1=∠2，∠A=∠F.
求证：∠C=∠D.
证明：因为∠1=∠2（已知），∠1=∠3（ ）
得∠2=∠3（ ）
所以AE//_______( )
得∠4=∠F（ ）
因为__________(已知)
得∠4=∠A
所以______//_______( )
所以∠C=∠D( )
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC中，∠A，∠B，∠C的对边分别为a、b、c，下列说法中错误的是（ ）
A．如果∠C－∠B＝∠A，则△ABC是直角三角形，且∠C＝90；
B．如果
，则△ABC是直角三角形，且∠C＝90；C．如果（c＋a）（ c－a）＝
，则△ABC是直角三角形，且∠C＝90；D．如果∠A：∠B：∠C＝3：2：5，则△ABC是直角三角形，且∠C＝90．
相关试题
